Sur les traces de Clairaut

Ce n’est pas parce qu’un mathématicien est considéré aujourd’hui comme une figure emblématique des sciences qu’il en a toujours été ainsi. Par exemple, Joseph Fourier (1768-1830) par ses travaux est, aujourd’hui, l’un des savants les plus connus au monde : pas un seul ingénieur n’ignore son nom ! Pourtant, dans la seconde moitié du XIX ^e siècle, il est largement ignoré. Qu’en est-il de Clairaut ? Les livres publiés, les journaux et les dictionnaires mathématiques de l’époque nous fournissent quelques indications.

Un auteur à succès

En consultant les productions des libraires-imprimeurs tout au long du XIX^e siècle, nous constatons que les Élémens de géométrie de Clairaut – le titre était ainsi écrit à l’époque – ont connu diverses rééditions : en 1830, en 1852, en 1853 et en 1861. À côté de ces reprises, notons également la parution, en 1833, des Élémens de géométrie d’après les élémens de Clairaut par Jean-Baptiste François Étienne Ajasson de Grandsagne (1802-1845).

Cette dernière édition connaît un certain succès puisque l’année suivante, en 1834, elle est rééditée. Il s’agit d’un ouvrage très pratique suivi d’une partie sur l’usage de « quelques instrumens de mathématiques, équerre, rapporteur, compas de proportion, etc. ».

En 1853, paraissent les Éléments de géométrie par Clairaut ; c’est une nouvelle édition mise en accord avec le système décimal par un certain Honoré Regodt, « professeur à l’association phylotechnique de Paris » et auteur de nombreux ouvrages de toutes sortes. Tout au long du XIX^e siècle, la géométrie de Clairaut a ainsi inspiré de nombreux auteurs. Il en est de même, sans doute dans une moindre mesure, pour ses Élémens d’algèbre qui connaissent une cinquième édition en 1824.

Son nom et ses contributions sont également régulièrement cités dans toutes les publications mathématiques spécialisées du XIX^e siècle (voir en encadré ci-dessous).

[encadre]

Les publications spécialisées

Au XVIII^e siècle, les sciences circulent par voie épistolaire ou par le biais des journaux savants qui contiennent des mémoires d’art, de littérature et, à la marge, de sciences. Le XIX^e est le siècle de la spécialisation de la presse : au début du siècle, il existe une seule publication mathématique – les Annales de mathématiques pures et appliquées dites « de Gergonne » du nom de son co-fondateur Joseph-Diaz Gergonne (1771-1859) devenu seul rédacteur après quelques mois d’activité – alors qu’en fin de siècle, ce chiffre s’élève à quelques dizaines. Aujourd’hui, il existe des milliers de journaux mathématiques.

Les Annales de Gergonne ayant cessé en 1832, il faut attendre 1836 pour voir le lancement du Journal de mathématiques pures et appliquées, souvent appelé ensuite Journal de Liouville par hommage à son fondateur, Joseph Liouville (1809-1882). Ce Journal peut être considéré comme le premier journal de recherches mathématiques français. Quelques années plus tard, Olry Terquem (1782-1862) et Camille Gérono (1799-1891) fondent les Nouvelles annales de mathématiques ou Journal des candidats aux Écoles polytechnique et normale. L’objectif est la préparation des élèves aux concours d’accès aux grandes écoles mais beaucoup d’articles dépassent le simple cadre scolaire.

Le champ éditorial français est ainsi essentiellement partagé entre un journal de recherches mathématiques (Journal de Liouville) et un journal destiné à l’enseignement (Nouvelles annales de mathématiques). Dans le dernier tiers du siècle, ce partage bipolaire est largement remis en cause avec le lancement de plusieurs autres publications spécialisées.

[/encadre]

Présentation d’Alexis Clairaut dans le Bulletin bibliographique (1861).

Dans les dictionnaires de mathématiques

Si Pierre Larousse (1817-1875) déclare que le XIX^e siècle est le « siècle des dictionnaires », force est de constater que peu de dictionnaires exclusivement destinés aux mathématiques ont été édités. Nous en avons repéré deux : le Dictionnaire des sciences mathématiques pures et appliquées d’Alexandre André Victor Sarrazin de Montferrier édité en trois volumes de 1835 à 1840 et le Dictionnaire des mathématiques appliquées comprenant les principales applications des mathématiques d’Hyppolite Sonnet paru en 1867. Ces deux dictionnaires ont eu un succès significatif puisque le Dictionnaire de Montferrier est réédité chez Hachette en 1845 ; celui de Sonnet connaît cinq éditions entre 1867 et 1895.

Les deux accordent une part importante à Clairaut. Le premier cite 56 fois le nom « Clairaut » et lui octroie une longue rubrique de quatre pages, pas forcément factuelle (voir ci-dessous).

Les premières lignes de la rubrique « Clairaut »
dans le Dictionnaire de Montferrier (1835).

Le Dictionnaire de Sonnet n’accorde pas de rubrique aux savants, mais souligne leurs apports. Ainsi le nom « Clairaut » est cité trois fois et il y a un renvoi au « Théorème de Clairaut d’après lequel l’aplatissement est égal aux 5/2 du rapport entre la force centrifuge et la pesanteur à l’équateur, diminué du rapport entre l’accroissement que subit le pendule à secondes en passant de l’équateur au pôle, et la longueur de ce pendule à l’équateur ».

Les dictionnaires de mathématiques d’aujourd’hui continuent à faire référence à Clairaut : celui d’Alain Bouvier, Michel Georges et François Le Lionnais (édition de 2001, Presses Universitaires de France) évoque dans leur entrée « Clairaut », les équations différentielles de Clairaut et « ses » équations aux dérivées partielles (voir encadré ci-dessous).

Notons que tous les textes ne retiennent pas les mêmes apports du savant : certains retiennent ses résultats en géométrie, d’autres en analyse.

[encadre]

Les équations différentielles de Clairaut

Le nom de Clairaut reste attaché à une équation différentielle qui, manifestement, ne constituait pas le centre de ses recherches. Avec les notations modernes, elle s’écrit y(x) = x y’(x) + f(y’(x)) où f est une fonction de classe C¹ (c’est-à-dire continument dérivable) sur un intervalle I de ℝ.

Elle est apparue à l’occasion d’un problème formulé dans un article, publié en 1734 dans les Mémoires de l’Académie royale. Le problème est le suivant : « Trouver les courbes MON autour desquelles, faisant glisser l’équerre MCN, le sommet C de cette équerre soit toujours dans la courbe donnée EC. »

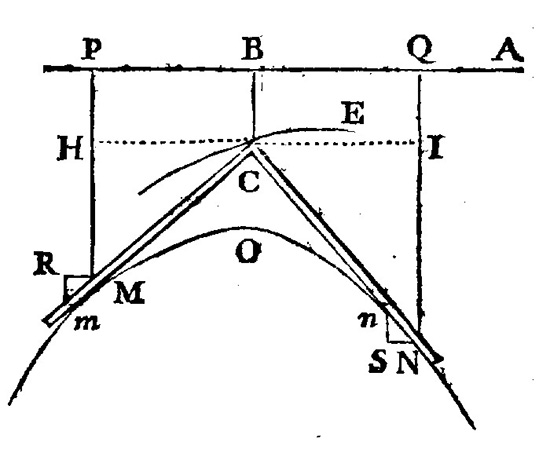
En fait, Clairaut indique qu’il s’agit d’une digression à ce problème. Il remarque que, pour cette équation, il existe une solution singulière. À la famille des solutions générales du type y(x) = mx + f(m), avec m appartenant à I, solutions représentées par des droites, il faut en adjoindre une autre dont la courbe représentative est l’enveloppe de cette famille de droites : c’est celle-ci qui est appelée singulière.

L’équation aux dérivées partielles de forme similaire,

 porte aussi le nom de Clairaut.

Daniel Lignon

[/encadre]