La géométrie des alvéoles

La cire fabriquée par les abeilles sert à bâtir les alvéoles des ruches permettant de protéger le couvain et de stocker la nourriture des abeilles. La construction des alvéoles se déroule sur chaque face d’un rayon disposé à la verticale. L’élaboration d’un rayon débute par le plafond de la ruche puis s’étend vers le bas. Le gâteau de cire est constitué par des alvéoles juxtaposées. La partie émergée de chacune des alvéoles est un hexagone régulier dont le côté mesure environ 3 mm. La profondeur d’une alvéole est de 11,5 mm et l’épaisseur de ses parois est d’environ 1/20 de mm. Chaque cellule est adossée à trois autres cellules au moyen d’une surface formée de trois losanges (rhombes). Les alvéoles ne sont en fait pas placées parfaitement à l’horizontale. Elles font un angle de 7 à 8 degrés vers le haut, pour éviter que le miel ne s’écoule hors des cellules par capillarité. Le gâteau de cire, par sa forme et son agencement, est gage d’une grande solidité.

Les alvéoles de cire.

Un cadre de ruche.
Optimisation ou propriété physique ?
Dans l’Antiquité, Aristote et Pline l’Ancien mentionnent la forme hexagonale des alvéoles. Ce dernier ose même un parallèle entre la forme observée et le fait que les abeilles ont six pattes ! La première étude mathématique de ce pavage date du iv e siècle : dans ses Collections, Pappus d’Alexandrie affirme que les abeilles adoptent la forme hexagonale par souci d’économie de cire et leur attribue une « intuition géométrique » pour parvenir à paver le plan. En 1661, l’astronome allemand Johannes Kepler (1571-1630) compare les alvéoles aux cristaux et écrit que les abeilles ont un « esprit mathématique ». En 1819, le physicien français René-Antoine
Ferchault de Réaumur (1683-1757) défend lui aussi l’idée que la forme hexagonale est motivée par un souci d’économie. Pourtant, une autre manière de concevoir le problème avait déjà vu le jour : en 1660, le mathématicien danois Rasmus Bartholin (1625-1698) avait émis l’hypothèse que la forme hexagonale n’avait rien d’extraordinaire mais était simplement due à la pression qu’exerce chaque abeille sur les parois du cadre. De fait, en 1859, Charles Darwin (1809-1882) remarque qu’au début de sa construction l’alvéole a une forme circulaire qui, à la fin du processus, devient hexagonale. Selon lui, l’explication n’est donc pas un problème d’optimisation, mais plutôt la conséquence de phénomènes physiques.

Rasmus Bartholin.
Modélisation des possibilités de pavage
Puisque les abeilles recouvrent une surface entière avec la cire, on peut modéliser mathématiquement le problème par une question de pavage du plan. Pour un polygone régulier convexe de n côtés (donc nécessairement n ≥ 3), l’angle au centre de tout côté vaut 360 ⁄n. Donc, l’angle complémentaire est égal à α = 180 – 360 ⁄n. Pour y accoler k polygones identiques (il est clair qu’il en faut au moins 3), il faut que k × α = 360. On a donc k × (180 – 360 ⁄n) = 360, ce qui donne 1 − 2/n = 2/k, soit enfin k = 2n/ (n − 2).
Étudions tous les cas possibles : on a soit n = 3 d’où k = 6 (ce qui fait 6 triangles équilatéraux) ; soit n = 4 d’où k = 4 (donc 4 carrés) ; soit n = 5 mais alors k n’est pas entier (pas de solution) ; soit n = 6 d’où k = 3 (donc 3 hexagones réguliers) ; enfin, si n = 7, alors k est non entier et inférieur à 3, il est donc inutile d’étudier les n plus grand. Conclusion : seuls des triangles équilatéraux, des carrés et des hexagones réguliers permettent ce pavage, ce qui rejoint le questionnement de Pappus d’Alexandrie. Pour chacune de ces formes, fixons arbitrairement une aire égale à 1.
Un triangle équilatéral d’aire 1 a un côté de longueur 2 / 3 1/4 et donc un périmètre de 6 / 31/4 ≈ 4,56.
Un carré d’aire 1 a un côté de longueur 1, et donc un périmètre de 4.
Enfin, un hexagone régulier d’aire 1 a pour côté
et donc pour périmètre 2 × 121/4 ≈ 3,72.
Le triangle équilatéral et le carré présenteraient trop d’espaces angulaires non utilisés pour les larves, qui sont elles-mêmes de forme circulaire ; l’hexagone, au contraire, se rapproche davantage du cercle et est à cet égard plus commode.
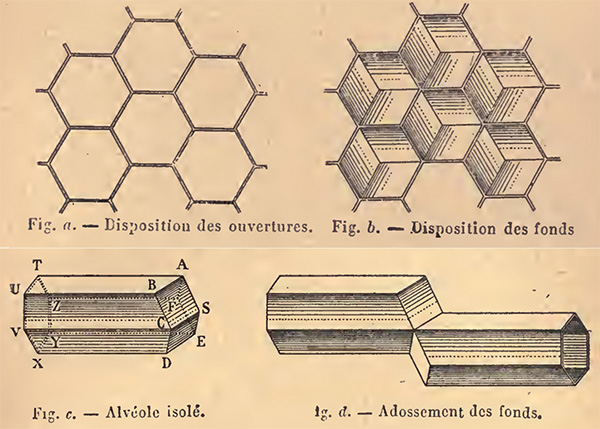
Formes des alvéoles d’abeille. Illustrations issues du livre d’Émile Fourrey,
Curiosités géométriques, Vuibert, 1907.
Des rhombes au don des alvéoles
Il est important de remarquer que les alvéoles, qui sont des éléments en trois dimensions et s’organisent de part et d’autre de la structure, ne se présentent pas de la même manière d’un côté et de l’autre : leur extrémité interne ne constitue pas un hexagone régulier. Il s’agit de 3 losanges qui s’emboitent les uns dans les autres pour former ce qu’on appelle les rhombes.
C’est par ces losanges que les prismes se raccordent et non pas par la surface hexagonale. Il semble que la forme rhomboïdale du fond n’ait été remarquée qu’au XVIIIe siècle, et que le mathématicien et astronome franco-italien Giovanni Domenico Maraldi (1709-1788) ait été le premier à déterminer expérimentalement avec précision les angles des losanges. En 1743, le mathématicien écossais Colin Maclaurin (1698-1746) reprend l’approche par le calcul différentiel de son collègue suisse Samuel Kœnig (1712-1757) et trouve, à la minute d’arc près, les angles de Maraldi.
Giovanni Domenico Maraldi.
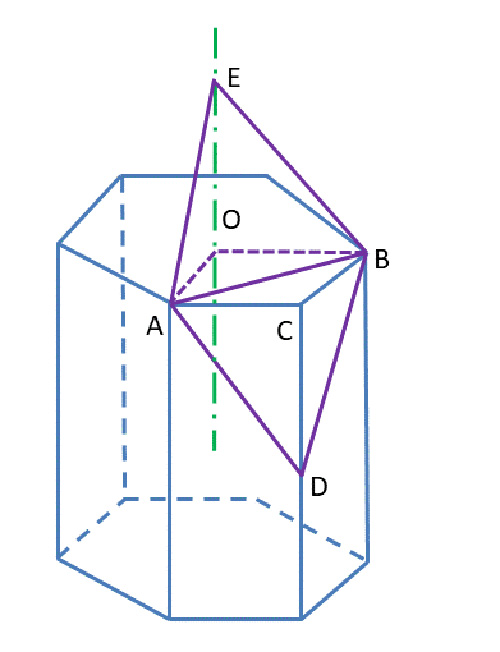
Alvéole de cire (entrée hexagonale en bas, fond rhomboïdal en haut ;
un seul rhombe ou losange est représenté).
Comme on peut le voir sur la figure ci-contre, l’hexagone de centre O, couvercle « naturel » du prisme, est remplacé par trois losanges de sommet commun E, situé sur l’axe. Considérons seulement un tiers du prisme et plaçons le point D, sur une arête, tel que
Le quadrilatère (EADB) remplace le losange (OACB) et est l’un des trois losanges de raccordement. Appelons P1 le tiers de prisme de couvercle naturel le losange (OACB) et P2 le tiers de prisme tronqué de couvercle le losange (EADB). Comparons les volumes de P1 et P2 ainsi que les aires de leurs enveloppes respectives. Tout d’abord, les volumes P1 et P2 sont égaux : les deux tétraèdres (DACB) et (EOAB) ont le même volume : le volume rajouté compense exactement le volume enlevé. Comparons maintenant les aires : couvercle et surfaces latérales.
Posons AC = BC = 1 ; d’où
Si h désigne la hauteur initiale du prisme non tronqué, et posant x = OE = CD, on trouve :
et
L’aire totale de P1 (2 rectangles et un losange) vaut
et l’aire totale de P2 (2 trapèzes et un losange) vaut 2h – x + Aire (EADB).
On a donc
et l’aire de P2 vaut par conséquent :
Pour x = 0 on retrouve bien
Il est facile de vérifier que la fonction x → f (x) atteint son minimum pour
Le minimum de cette aire totale étant inférieur à l’aire de P1, les abeilles choisissent bien la solution la plus économique…
Cette valeur de x permet d’obtenir et
On a donc, dans le triangle (EAB) :
soit = arccos (− 1/3) ≈ 109,471° ≈ 109°28’, qui est précisément la valeur obtenue par MacLaurin en 1743 !
Il est amusant de noter que c’est également l’angle entre deux liaisons C − H dans la molécule de méthane CH4…
Ainsi, l’adossement des cellules permet déjà de supprimer un fond : de plus l’hexagone est celui qui, pour une surface donnée, a le plus petit périmètre et qui, par conséquent, exige le moins de cire pour les parois. Enfin, les dimensions adoptées par les abeilles pour le fond rhomboïdal (formé de losanges) correspondent à la plus petite surface totale pour l’alvéole et donc à la plus petite quantité de cire.
Les travaux de László Fejes Tóth
Beaucoup plus tard, en 1943, le mathématicien hongrois László Fejes Tóth (1905-2005) démontre, en faisant l’hypothèse de convexité des tuiles du pavage, que le pavage hexagonal régulier donne la partition du plan en surfaces égales ayant le plus petit périmètre. Ce n’est qu’en 1999 que Thomas Hales (né en 1958), de l’université du Michigan, présente la preuve générale (de 19 pages) du théorème du nid d’abeille (« The Honeycomb conjecture »), montrant que ce résultat est toujours vrai (même sans l’hypothèse de convexité). C’est également Hales qui a démontré la conjecture de Kepler sur la meilleure façon d’empiler des sphères (problème bien connu des marchands de fruits lorsqu’ils rangent les oranges sur leur étal).
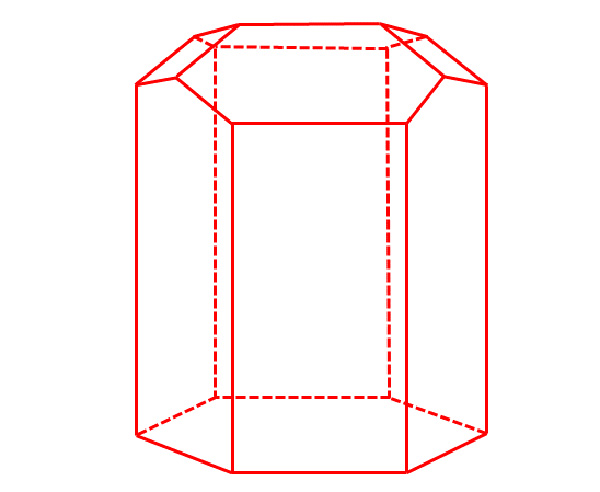
La géométrie optimale proposée par Tóth (entrée hexagonale en bas, fond en haut).
En 1964, Tóth parvient à montrer que, même si la structure hexagonale régulière reste en pratique la plus efficace, il existe une autre forme qui permettrait une occupation encore meilleure de l’espace en faisant économiser aux abeilles 0,35 % de cire. En 1994, soit trente ans plus tard, Denis Weaire et son élève Robert Phelan, du Trinity College de Dublin, étudient les films de savon. En injectant une solution savonneuse entre deux lames de verre, ils obtiennent précisément la forme de Tóth, qui serait donc une forme minimale.
Toutefois, ils remarquent qu’en épaississant les parois des alvéoles, la structure des fonds bascule brutalement sur celle adoptée par les abeilles. Ainsi ces dernières utiliseraient bien la forme optimale, les parois n’ayant pas une épaisseur négligeable comme dans l’étude mathématique du problème. On peut se demander ce qu’il en serait si les côtés des alvéoles étaient incurvés, c’est-à-dire si on n’imposait pas aux cellules d’être des prismes droits hexagonaux réguliers. Il reste donc à résoudre le problème en ne fixant que les contraintes d’aire d’entrée et de volume de l’alvéole.

Structure de Weaire–Phelan, basée sur des octaèdres tronqués (polyèdres possédant 8 faces hexagonales régulières, 6 faces carrées, 24 sommets identiques et 36 arêtes égales).
Plus ingénieures que mathématiciennes ?
En 2013, le professeur indien Bhushan Lal Karihaloo et son équipe de l’université de Cardiff confirment l’hypothèse de Darwin. Les alvéoles ont à l’origine une forme circulaire et ensuite, sous l’effet de la chaleur de la ruche (qui peut aller jusqu’à 45°C du fait du grand nombre d’abeilles et de leur activité frénétique), conformément au principe de la viscoélasticité, elles se compriment entre elles, la cire fondant et s’écoulant lentement, tel un caramel. Des angles commencent alors à se former mécaniquement et la forme circulaire devient hexagonale. L’écoulement de cire viscoélastique fondue près de la triple jonction entre les cellules circulaires voisines peut être libre ou contraint par la cire non fondue loin de la jonction. La chaleur nécessaire à la fusion de la cire est fournie par les ouvrières. En outre, dans les nids naturels, les ouvrières doivent régulièrement passer d’une taille de cellule à l’autre, fusionner des alvéoles imparfaites et optimiser la construction dans des géométries contraintes. Ces obstacles sont des défis pour les ouvrières. Agissent-elles en tant qu’architectes ou en simples automates dont le rôle est de répliquer une forme parfaite ?
En utilisant une analyse d’image automatisée pour extraire les irrégularités dans la construction des nids naturels, les chercheurs Michael Smith, Robert Napp, et Nils Petersen de l’université d’Auburn (Alabama) ont montré que certaines configurations de construction sont plus difficiles pour les abeilles que d’autres, et que les ouvrières surmontent ces défis en construisant des cellules de taille intermédiaire et en modifiant progressivement leur inclinaison. De manière remarquable, en anticipant ces défis de construction, les ouvrières réalisent des fusions de haute qualité grâce à une détection locale procédant d’une optimisation globale. Contrairement aux automates qui construisent des hexagones parfaitement répliqués, ces irrégularités de construction montrent le rôle actif des ouvrières dans la formation de leur nid et les véritables capacités architecturales des abeilles mellifères. Les structures en nid d’abeille ont trouvé des applications étendues dans divers domaines, comme l’architecture, les transports, le génie mécanique, le génie chimique, les nanotechnologies et, récemment, la biomédecine.
Jean-Christophe Pain est membre du laboratoire Matière en conditions extrêmes, au sein du centre de recherche CEA Paris-Saclay.