Des abeilles à la dyscalculie

By

Catherine Thevenot est professeure à l’institut de psychologie de l’université de Lausanne où elle codirige le Laboratoire du cerveau et du développement cognitif. Spécialisée dans l’apprentissage et le développement des compétences numériques chez les enfants, elle s’intéresse aux abeilles pour identifier les mécanismes biologiques innés dans ces apprentissages.

Catherine Thevenot.

Tangente : Quels sont vos projets de recherche actuels ?

Catherine Thevenot : Je travaille beaucoup en ce moment sur le comptage sur les doigts. Nous avons des résultats spectaculaires sur l’intérêt d’enseigner une telle méthode chez des enfants de 5 ans. Je travaille également sur la relation entre nombre et espace ainsi que sur la manière dont les adultes résolvent des multiplications. J’ai une trentaine de projets en cours dont beaucoup tournent autour de ces thématiques.

Quelle place occupe les abeilles dans vos recherches ?

J’ai travaillé sur les abeilles avec mes collègues Martin Giurfa et Rosa Rugani dans le cadre de mes recherches sur la relation entre nombre et espace. Martin est l’un des plus grands spécialistes au monde des abeilles, avec une approche plus biologique que la mienne, et Rosa avait déjà démontré les capacités des poussins à organiser les quantités de gauche à droite.

Abeille domestique Apis Mellifera.

Vous vous intéressez donc à la manière dont les abeilles organisent et perçoivent les nombres dans l’espace. Comment procédez-vous ? 

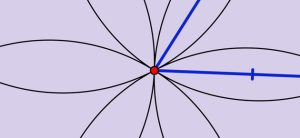
Une étude menée chez les abeilles a montré qu’elles organisent spontanément les quantités selon un axe spatial gauche-droite. Après avoir été entraînées à reconnaître une quantité cible (par exemple, trois éléments), les abeilles sont confrontées, lors du test, à deux ensembles identiques ne correspondant pas à la quantité apprise (par exemple, un élément à gauche et un élément à droite, ou cinq à gauche et cinq à droite). De manière significative, elles se dirigent plus fréquemment vers l’ensemble situé à gauche lorsqu’il contient une quantité inférieure à la cible, et vers celui situé à droite lorsqu’il contient une quantité supérieure. Ce comportement suggère l’existence d’une représentation spatiale des quantités, où les petites valeurs sont associées à la gauche et les grandes à la droite.

Quel est l’enjeu de ces recherches ?

Le fait que les êtres humains qui écrivent de gauche à droite organisent également mentalement les nombres de gauche à droite est connu depuis des décennies. Mais une grande question est de savoir si cette organisation mentale est purement culturelle. Dans des cultures où les individus écrivent de droite à gauche, les nombres ont plutôt tendance à être aussi organisés mentalement de droite à gauche, ce qui est un argument pour dire que la culture est responsable de l’organisation mentale des nombres. Or, chez des bébés ou des poussins, qui ne sont pas imprégnés de la culture de la lecture, il est mis en évidence une préférence pour l’organisation des petites quantités à gauche et des plus grandes à droite. Nous avons alors voulu savoir si ce résultat était aussi observable chez des insectes, et c’est le cas ! Nous pouvons donc conclure que l’organisation gauche-droite des quantités repose sur des bases biologiques mais que nos représentations innées sont modulées par la culture. Ces recherches sont importantes car déterminer quelle est l’organisation la plus naturelle pour les enfants pour se représenter les nombres permettra de concevoir des programmes d’apprentissage adaptés. Nos recherches confirment par exemple que l’utilisation classique de lignes numériques orientées de gauche à droite dans les classes est une bonne idée. Bien sûr, lors des premiers apprentissages, l’aspect ordinal du nombre, le fait que 3 soit après 2 par exemple, doit être articulé à sa dimension cardinale, le fait que 3 comprend 2.

Abeille charpentière Xylocope butinant une fleur de genêt.

Quelles techniques utilisez-vous pour explorer le cerveau humain ? 

Pour étudier l’apprentissage chez l’enfant et l’adulte, j’utilise des méthodes d’observation des comportements et des enregistrements des activations cérébrales. Chez l’abeille, pour l’instant, nous nous sommes limités à l’observation de son comportement. En revanche, des activations cérébrales ont été mises en évidence, qui évoluent au fur et à mesure du développement et de l’apprentissage chez des enfants de 8 ans, de 13 ans et des adultes pour la résolution de problèmes arithmétiques.

Justement, de quelle manière pouvez-vous définir les procédures automatisées de comptage ? 

Lorsque vous résolvez une addition très simple comme 2 + 3, vous n’avez pas l’impression de compter, la réponse surgit directement dans votre esprit. Les chercheurs ont longtemps pensé que cette résolution rapide était permise grâce au fait qu’après de nombreuses résolutions, la connaissance 2 + 3 était stockée en mémoire à long terme. Elle aurait alors le même statut que de savoir que Paris est la capitale de la France. Or, dans mes études, nous montrons que ce que les experts font pour résoudre ce type de problème n’est pas la récupération d’un fait en mémoire. Ils mettent en fait en place une procédure de comptage extrêmement rapide et inconsciente. Cette procédure revient à faire des petits pas de 1 sur une ligne mentale orientée de gauche à droite, d’où le rapport avec mes travaux sur les abeilles.

Dans ce cadre, les « experts » sont les individus qui ont automatisé les procédures, en général à l’âge de 13 ans. Établir ce que les experts font exactement lorsqu’ils résolvent des calculs est crucial pour mettre en place des méthodes d’apprentissage adaptées chez les jeunes enfants. Ainsi, la conclusion de mes travaux est que ce n’est pas une bonne idée de faire apprendre aux enfants des tables d’addition par cœur, comme cela est parfois fait dans certaines écoles. Ce qu’il faut privilégier, c’est le comptage, sur les doigts par exemple.

L’usage généralisé des calculettes et des moyens technologiques a profondément transformé notre quotidien. Le comptage sur les doigts reste-t-il une étape nécessaire au développement des habiletés numériques ? 

Ce que nous montrons est qu’il n’y a que très peu d’enfants qui peuvent faire des calculs mentaux aisément sans être passés par une étape de calcul sur les doigts. Donc, sans être nécessaire au bon développement des compétences arithmétiques, oui, le calcul sur les doigts est une étape importante. Une calculatrice devrait être fournie aux enfants le plus tard possible dans leur cursus scolaire car il est extrêmement important que les enfants puissent manipuler les nombres, compter, calculer pour finalement pouvoir automatiser leurs procédures de calcul. Un enfant qui sait que 7 × 6 = 42 sera toujours plus rapide que celui qui devra sortir sa machine à calculer. Le temps et les ressources cognitives économisés sur l’accomplissement du calcul pourront être utilisés pour des activités plus intéressantes et de plus haut niveau comme saisir l’énoncé mathématique dans lequel le calcul est intégré, comprendre le principe géométrique de calcul d’une surface. En d’autres termes, les enfants qui ne peuvent pas résoudre automatiquement des calculs simples auront moins de chance de développer des compétences mathématiques avancées, de raisonner efficacement face à des problèmes complexes et d’aborder sereinement des concepts abstraits.

Pourriez-vous nous présenter le déroulement d’une séance d’observations chez les enfants ? 

La grande majorité des observations que nous faisons sur des enfants se fait dans leurs écoles, et nous incluons tous les enfants correspondant à nos âges d’intérêt. Parfois après coup, nous excluons de nos analyses des enfants allophones* qui n’auraient pas compris nos consignes, ou, en fonction des objectifs de nos recherches, des enfants qui présenteraient des troubles des apprentissages. (* Une personne allophone est une personne dont la langue maternelle est différente de la langue utilisée dans l’expérience). Parfois, ce sont précisément ces enfants qui nous intéressent, notamment s’ils présentent une dyscalculie. Nous pouvons proposer aux enfants de résoudre de petits calculs simples, c’est-à-dire avec des nombres à un chiffre, et nous les filmons pour ensuite coder leurs comportements. Beaucoup de mes études utilisent également les temps de réaction et, dans ce cas, les tâches numériques sont présentées sur un ordinateur. En ce qui concerne les études en imagerie cérébrale, que j’effectue en collaboration avec mon collègue Jérôme Prado basé au centre de recherche en neurosciences à Lyon, les procédures sont plus compliquées. Les enfants doivent se rendre au laboratoire de recherche avec leur famille. Avant la passation réelle de l’expérience dans le scanner, l’enfant est familiarisé avec le dispositif afin de lui permettre de s’habituer à l’environnement, au bruit fait par la machine IRM (Imagerie par résonance magnétique) et à l’exigence d’immobilité durant l’étude. Des scanners imitant des fusées, par exemple, sont souvent utilisés pour rassurer les enfants et donner un aspect ludique à la situation.

Concernant la dyscalculie, où en est-on ?

La dyscalculie est un trouble du développement des acquisitions des connaissances liées au nombre et à l’arithmétique. Elle touche 3 à 6 % des enfants et ses origines sont en partie génétiques.

Plusieurs hypothèses peuvent expliquer les troubles qu’elle engendre. Pour certains chercheurs, elle constitue un trouble primaire consécutif à une difficulté à appréhender les nombres sous leur format non symbolique ou bien à une difficulté à faire la correspondance entre le format non symbolique et le format symbolique (par exemple, I I I correspond au symbole « 3 »). Pour d’autres chercheurs, elle correspond plutôt à un trouble secondaire lié, par exemple, à des déficits des capacités en mémoire de travail, des compétences visuo-spatiales et de l’inhibition, ou bien encore, et c’est ce qui sera développé ici, de l’automatisation procédurale. Toutes ces hypothèses ne sont d’ailleurs pas forcément mutuellement exclusives.

L’hypothèse du déficit d’automatisation procédurale explique l’un des plus grands obstacles que les enfants dyscalculiques rencontrent dans le développement de leurs compétences numériques, à savoir leur difficulté à résoudre facilement des problèmes arithmétiques. Récemment, nous avons montré que ces difficultés sont encore plus apparentes pour l’addition par rapport à la multiplication. Ainsi, les difficultés des enfants dyscalculiques se situeraient plutôt à un niveau procédural qu’à un niveau mémoriel. En effet, alors que les résultats des multiplications sont appris par cœur et donc finalement stockés en mémoire à long terme, il n’en est pas de même des additions qui sont entraînées dans les petites classes par le biais du comptage.

Les enfants commencent effectivement à résoudre des additions en égrainant la chaîne numérique de 1 en 1, bien souvent en s’aidant de leurs doigts. L’addition 2 + 3, par exemple, est classiquement résolue en représentant 2 sur une main, 3 sur l’autre et en recomptant tous les doigts levés à partir de 1 (c’est-à-dire 1, 2 ; 1, 2, 3 et donc 1, 2, 3, 4, 5). Au fur et à mesure du développement, ces stratégies de comptage se simplifient, en partant du plus grand des opérandes (dans notre exemple, on part de 3 et on compte : 4, 5). Selon la théorie du comptage automatisé, ces procédures ne disparaissent jamais complètement et même l’expert adulte résout les petites additions par des procédures de comptage, devenues si rapides qu’elles ne sont plus accessibles à la conscience. Cette automatisation des procédures, qui correspondrait donc à la signature du fonctionnement expert dans le domaine de la résolution de problèmes arithmétiques, apparaîtrait vers l’âge de 12-13 ans chez l’enfant sans trouble des apprentissages.

Ainsi, le problème majeur des enfants dyscalculiques, ou tout au moins de certains enfants dyscalculiques, pourrait se situer dans leur échec à automatiser les procédures de comptage. Cette hypothèse explique leur lenteur dans l’exécution des opérations et le coût cognitif qui demeure élevé pour cette exécution en comparaison à des enfants non dyscalculiques qui résolvent les mêmes opérations très rapidement, pratiquement sans effort.

Les observations sur les abeilles jouent-elles un rôle dans l’étude de la dyscalculie ?

Ces travaux, menés chez une espèce non humaine et non verbale, suggèrent que certaines bases de la cognition numérique, comme l’organisation spatiale des quantités, ou des procédures inconscientes de calcul, pourraient reposer sur des mécanismes biologiques élémentaires, partagés entre espèces. Dans le contexte de la dyscalculie, cela permet de mieux cerner les composantes fondamentales du sens du nombre, indépendamment du langage ou de l’enseignement formel. En identifiant les biais d’organisation spatiale qui sous-tendent la représentation des quantités, ces recherches pourraient aider à concevoir des outils pédagogiques adaptés, visant à renforcer ces représentations spatiales précoces chez les enfants en difficulté. Par exemple, des interventions ludiques mobilisant l’axe gauche-droite ou la manipulation d’espaces numériques concrets pourraient contribuer à soutenir le développement du sens du nombre et à compenser certaines fragilités observées chez les enfants dyscalculiques.

Des abeilles dessinées dans le Bestiaire de Northumberland, écrit vers 1250-1260, Getty Museum.

Quelles sont les avancées des connaissances sur le rôle de la mémoire dans les apprentissages ?

Il n’y a pas d’apprentissage sans attention et sans mémoire. Ces deux piliers cognitifs sont à la base de tout apprentissage. Si on ne peut pas porter notre attention sur une information, jamais elle ne passera en mémoire. Si on souffre d’un désordre mémoriel, l’information à laquelle on aura été attentif disparaîtra rapidement et pour toujours de notre univers cognitif. Les interactions entre mémoire et attention sont donc au cœur de toute recherche sur l’apprentissage. Cependant, des recherches récentes montrent que les méduses, qui n’ont pas de système nerveux central donc pas de cerveau, peuvent apprendre par associations. La possibilité de cet apprentissage, bien que très basique, est surprenante pour les chercheurs qui devront comprendre comment il est possible sans capacités attentionnelles et mémorielles gouvernées par le cerveau.

Abeille domestique Apis Mellifera butinant une fleur de campanule.

À quel âge perçoit-on l’émergence du raisonnement chez l’être humain ?

Les enfants, dès la naissance, ont des intuitions impressionnantes concernant leur environnement. Ils sont étonnés, par exemple, qu’une chaise se déplace toute seule, que 1 + 1 puisse faire 1 (à travers des tours de magie par exemple) ou qu’un objet solide en traverse un autre. Cependant, on ne parle pas encore de raisonnement à cet âge-ci. Ce n’est qu’à partir de l’âge de 5-6 ans que les enfants vont pouvoir commencer à raisonner sur des situations concrètes, c’est-à-dire impliquant des objets ou des images. Il faudra cependant encore attendre plusieurs années avant qu’ils ne puissent raisonner sur des hypothèses ou des concepts abstraits.

Propos recueillis par Mireille Schumacher