Quelques constructions
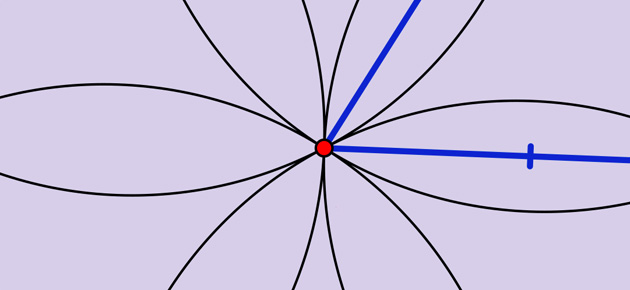
Nous verrons que tous les polygones réguliers ne sont pas constructibles à la règle et au compas, mais la plupart le sont (voir l’article Heptadécagone : le vrai et le faux). Voici quelques constructions qui permettent d’inscrire un polygone dans un cercle de centre O et de rayon R.
L’hexagone
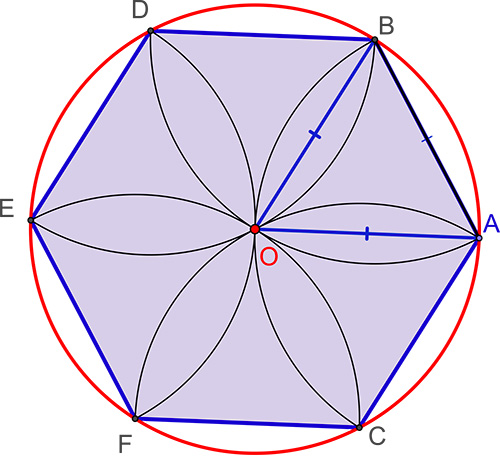
Le tracé de l’hexagone est bien connu de tous les écoliers en quête de rosaces. Il suffit de reporter le rayon du cercle pour construire un hexagone régulier. Le cercle de centre A et de rayon R coupe le cercle premier en B et C. Le triangle OAB est équilatéral. Les symétriques de A, B et C permettent d’obtenir l’hexagone ABDEFC, qui se décompose en six triangles équilatéraux.
Le triangle équilatéral
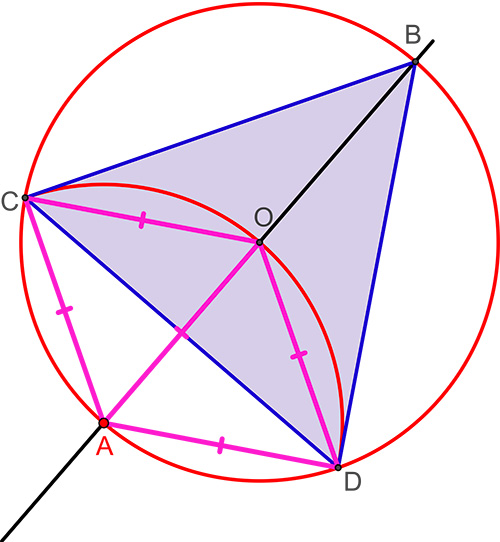
La construction du triangle équilatéral se déduit directement de la construction précédente. Pour inscrire un triangle équilatéral au cercle de centre O et de rayon R, tracez un diamètre [AB]. Le cercle de centre A et de rayon R coupe le premier cercle en C et D. Les triangles AOD et AOC sont deux des six triangles composant l’hexagone de la figure précédente. Le triangle BDC est le triangle équilatéral recherché.
Le carré
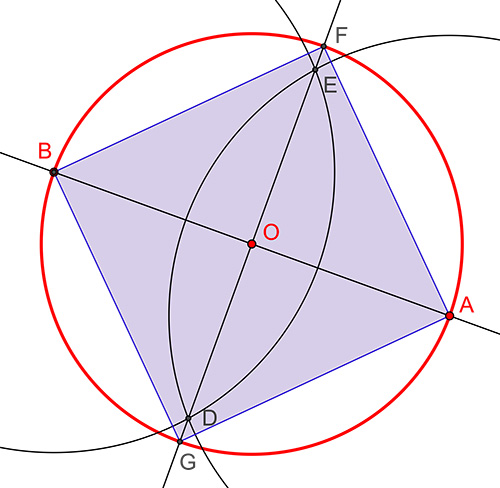
Pour inscrire un carré dans un cercle de centre O et de rayon R, coupez le cercle par un diamètre [AB].
Tracez un cercle de centre A et de rayon plus grand que R. Tracez un cercle de centre B et de même rayon. La droite passant par les intersections E et D des deux cercles, qui est la médiatrice de [AB], coupe le premier cercle en F et G. AFBG est le carré recherché.
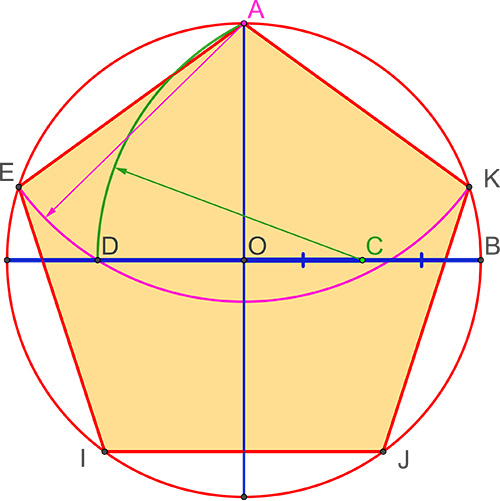
Le pentagone
Le premier polygone régulier, non trivial à tracer, inscrit au cercle de centre O, est le pentagone.
Tracez deux rayons perpendiculaires [OA] et [OB] du cercle de départ (voir la construction du carré). Tracez le milieu C de [OB] (voir la construction du triangle équilatéral).
Tracez le cercle de centre C et de rayon CA, il coupe la droite (OB) en D. Tracez le cercle de centre A de rayon AD, il coupe le cercle premier en E et K. Les segments [EA] et [AK] sont les deux premiers côtés du pentagone.
En les reportant viennent les points I et J. Le pentagone AEIJK de côté est le polygone recherché.
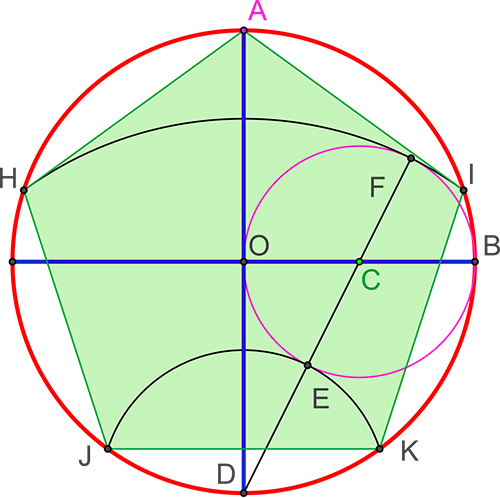
Il existe une autre construction classique.
Tracez un diamètre [AD] et un rayon [OB] perpendiculaire du cercle premier (voir la construction du carré). Tracez le milieu C de [OB]. Tracez le cercle de centre C et de rayon OC. La droite (DC) coupe le petit cercle en E et F. Les cercles de centre D passant par E et F coupent le cercle premier en H, I, J et K. Le pentagone recherché est AHJKI.
Tous les polygones avec un nombre pair de côtés sont constructibles à partir du polygone possédant un nombre moitié de côtés. Ainsi l’octogone est constructible à partir du carré.
On peut également s’intéresser aux problèmes de constructions inverses, obtenir tout le polygone à partir de la donnée d’un côté (voir en encadré). Cela suppose la détermination du cercle circonscrit au polygone.
[encadre]
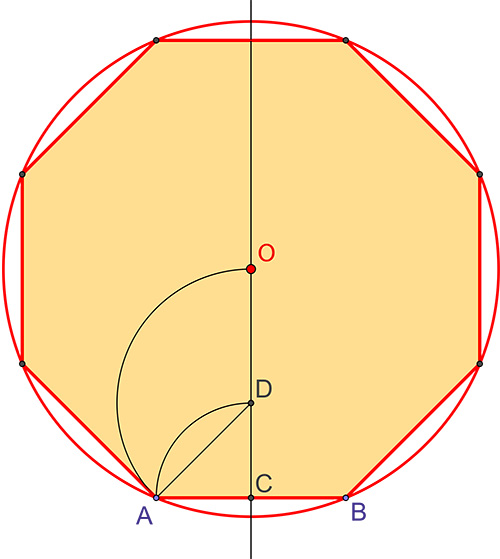
À partir du côté
Il est possible de construire un octogone ayant un côté AB donné. La construction présentée est empruntée à Léonard de Vinci (document Windsor RL 12542 de la Royal Library).
Tracez la médiatrice du segment [AB], elle le coupe en C.
Reportez AC sur la médiatrice. Reporter AD sur la médiatrice à partir de D, cela donne le point O, centre du cercle circonscrit, en reportant la longueur AB sur la circonférence on obtient l’octogone recherché.
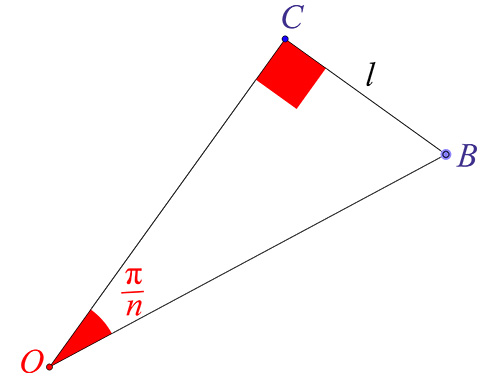
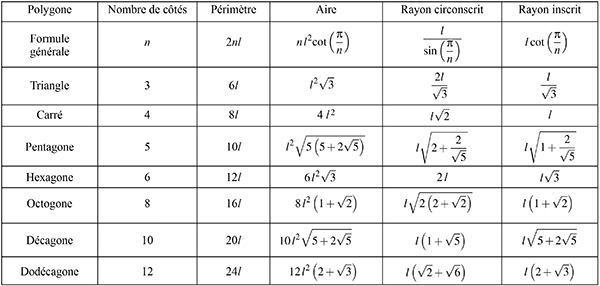
Le tableau ci-dessous indique les rayons circonscrit – OB – et inscrit – OC – d’un polygone de n côtés de demi-longueur l = CB.
[/encadre]












