Les polygones réguliers

Il paraît naturel de dire qu’un polygone régulier est un polygone dont tous les côtés ont la même longueur et dont les angles entre deux côtés consécutifs sont tous de même mesure. Par exemple un carré est un polygone régulier, alors qu’un rectangle (non carré) n’est pas un polygone régulier. De même un losange (non carré) n’est pas, non plus, un polygone régulier. Cette définition générale peut être scindée en deux, avec des termes modernes, pour mettre en évidence différents types de régularité.
Un polygone est dit isogonal si deux sommets quelconques se correspondent par une isométrie du polygone. Une conséquence est que l’angle entre deux côtés consécutifs est toujours de même mesure. Un rectangle est un exemple de polygone isogonal, tous ses angles étant droits.
Un polygone est dit isotoxal (du grec toxou, « arc ») si deux côtés quelconques se correspondent par une isométrie du polygone. Ainsi, tous les côtés sont de même longueur. Un losange est un exemple de polygone isotoxal.
Les polygones isotoxaux sont duaux des polygones isogonaux (voir en encadré).
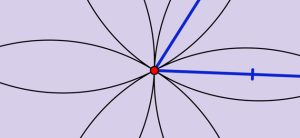
Un polygone est régulier si et seulement s’il est à la fois isotoxal et isogonal. Le triangle équilatéral, le carré ou le pentagone régulier sont des polygones réguliers convexes. Plus exotique, le polygone ci-dessous possède une symétrie d’ordre 10, est bien isogonal mais n’est pas régulier (on notera qu’il n’est pas isotoxal : ses côtés sont de deux longueurs différentes).
[encadre]
Dualité
La dualité est ici une opération qui, à chaque sommet d’un polygone, associe le côté d’un autre polygone. Ainsi, en reliant les milieux des côtés d’un losange, on obtient un rectangle et inversement. Le rectangle et le losange sont duaux l’un de l’autre.
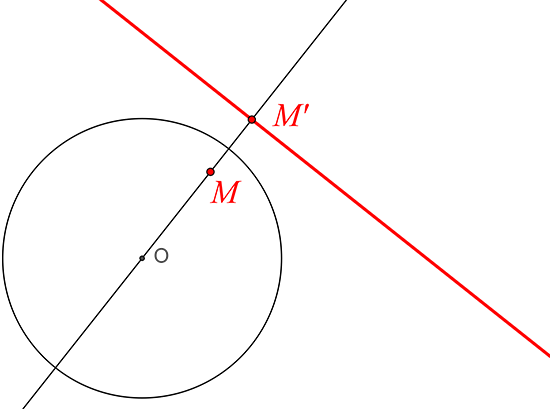
L’inversion par rapport à un cercle de centre O est un exemple d’opération de dualité qui transforme un point en une droite. La droite duale d’un sommet M par rapport à un cercle de centre O, de rayon R est la droite perpendiculaire à la droite O, passant par le point M ‘ telle que
[/encadre]
Utiliser la notation de Schläfli
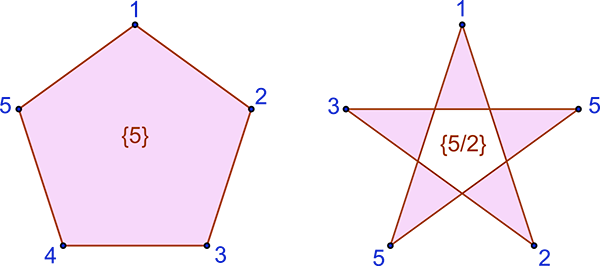
Le mathématicien suisse Ludwig Schläfli (1814-1895) a inventé une notation qui synthétise les principales propriétés des polytopes réguliers. On rappelle que les polytopes sont des polyèdres de dimension n. De ce point de vue, les polygones sont des polytopes en dimension 2. Le symbole de Schläfli pour un polygone régulier convexe à n côtés est {n}, ce qui peut paraître trivial. Par exemple {3} désigne un triangle équilatéral, {4} un carré…
La simplicité de cette notation ne fait que traduire la simplicité de construction d’un polygone convexe régulier. Il faut en fait comprendre le symbole {n} comme {n/1}, qui signifie que pour n sommets répartis régulièrement sur un cercle, les sommets se suivent dans l’ordre de leur disposition sur le cercle. Ainsi, après le sommet i, vient le sommet i + 1.
La notation générale de Schläfli permet de définir le cas particulier des polygones étoilés avec le symbole {n/k}. Toujours avec n sommets régulièrement répartis sur une circonférence, on construit cette fois-ci les côtés en passant du sommet i au sommet i + k (modulo n).
Par exemple, si la notation {5} symbolise le pentagone régulier, {5/2} représente le pentagramme.
Le cas {3/1} correspond au triangle équilatéral et {3/2} donne un triangle équilatéral parcouru dans l’autre sens (essayez !). Au sens de parcours près, nous pouvons donc en général restreindre notre étude à k ≤ n/2.
La plupart des auteurs, comme Louis Poinsot (1777-1859), limitent les étoiles aux cas où k et n sont premiers entre eux. Ce qui n’est pas la position de Meister (1724-1788) qui obtient des objets exotiques mais néanmoins parfaitement définis.
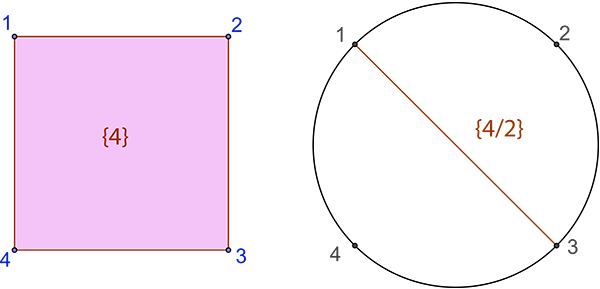
Pour {4} nous avons le carré. {4/2} correspond à 4 segments superposés, c’est-à-dire le parcours des sommets 1, 3, 1, 3 (les sommets 2 et 4 du premier carré n’étant pas pris en compte).
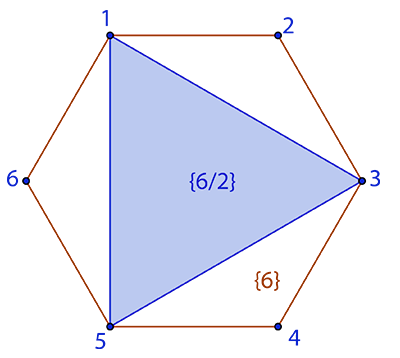
Un autre exemple : {6/2} est constitué de deux triangles superposés formés par la suite des sommets 1, 3, 5, 1, 3, 5.
Métamorphoses
Le mathématicien israélien Branko Grünbaum (1929-2018) a développé un procédé pour produire des polygones isogonaux. On considère alors les n points placés sur une circonférence ayant pour angle
par rapport à l’axe des abscisses, où n et k sont les entiers précédemment définis, j le numéro d’un des sommets, t est un paramètre réel positif.
En faisant varier le paramètre t, on obtient une suite continue de polygones isogonaux. Pour t = 0 nous débutons avec un polygone {n/k} c’est-à-dire un polygone régulier (convexe pour k = 1 et non convexe sinon). Pour t = n/4, le polygone est de nouveau régulier, il est de type {n/e} avec e = n/2 − k. Au-delà de cette valeur n/4 pour k, on retrouve les mêmes polygones que précédemment mais dans l’ordre inverse. Le terme (−1) j permet de s’écarter de façon symétrique du polygone régulier.
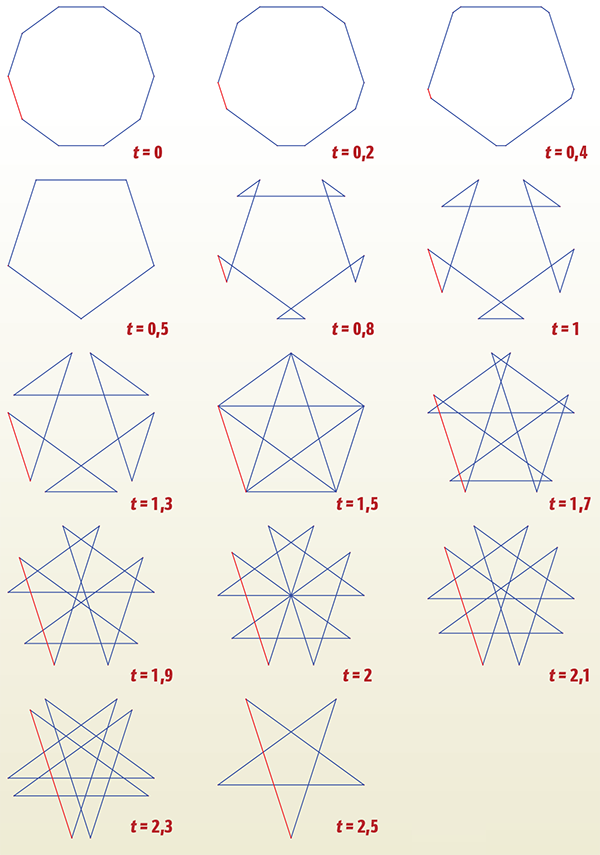
La métamorphose du {10 / 1} en {10 / 2} (de t = 0 à t = 5 / 2).
Par dualité, on peut obtenir de même des suites continues de polygones isotoxaux.
On notera que, pour certaines valeurs de t, les sommets se superposent. Mais interdire la superposition des sommets éliminerait la possibilité d’une visualisation de la continuité de cette jolie métamorphose.