La géométrie des courbes
Le livre Recherches sur les courbes à double courbure traite d’un sujet innovant. Depuis le XVIIe siècle, les géomètres de toute l’Europe ont étudié de nombreuses courbes du plan appliquant les idées de Descartes sur l’utilisation des coordonnées, puis les méthodes révolutionnaires du calcul différentiel et intégral de Newton et de Leibniz. Ils ont eu peu l’occasion d’envisager les courbes de l’espace ; on note cependant une communication à l’Académie des sciences d’Henri Pitot (1695-1771). Dans un mémoire de 1724, cet ingénieur hydraulicien étudie une sorte d’hélice et termine en écrivant : « Peut-être que ces sortes de courbes à double courbure, ou prises sur la surface des solides, seront un jour l’objet des recherches de géomètres. » Un défi qu’Alexis Clairaut s’empresse de relever.
Un premier livre innovant
Dans sa préface, il explique comment il va s’y prendre : une courbe de l’espace peut s’étudier en considérant ses projections sur les plans d’un angle solide (on dirait maintenant les trois plans d’un trièdre). Deux de ces projections suffisent et la courbe de l’espace participe « pour ainsi dire toujours de la courbure de ces deux courbes » ; c’est cela qui justifie l’expression « courbes à double courbure ».
L’ouvrage est, encore aujourd’hui, agréable à lire : il faut pour cela s’équiper de papier, d’un crayon et d’un logiciel de géométrie dynamique. Clairaut donne en effet de très nombreux exemples. Dans une première partie, il étudie des exemples de courbes à double courbure données par deux projections sur les plans de coordonnées, faisant comprendre que la courbe est alors intersection des deux cylindres construits à partir de ces projections. Dans ses exemples, les projections sont souvent des coniques. Il est intéressant d’imaginer nous-mêmes à quoi ressemble la courbe à partir de ses projections… Regardons, par exemple, les figures suivantes.
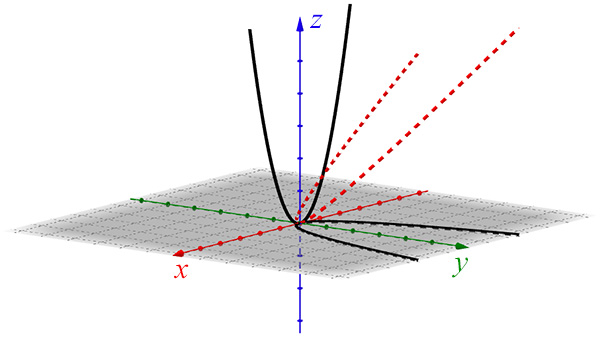
Les deux paraboles ont pour équation y = x ²
dans le plan O x y et z = x ² dans le plan O x z.
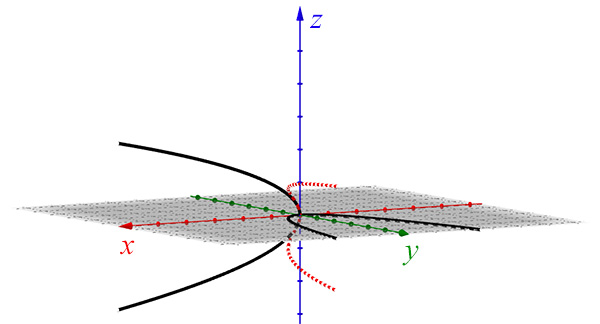
Les deux paraboles ont pour équation y = x ²
dans le plan O x y et x = z ² dans le plan O x z.
Clairaut insiste : une seule équation représente une surface, et non une courbe. Ainsi, l’équation y = x 2 représente, dans l’espace, le cylindre construit sur la parabole y = x 2 du plan Oxy. Clairaut en profite pour rappeler les équations de nombreuses surfaces, le plus souvent définies à partir de coniques. Au passage, il montre que toute équation homogène – c’est une équation de la forme f (x,y,z) = 0 telle que pour tout k, f (kx,ky,kz) = k nf (x,y,z), où n est une constante – est l’équation d’un cône de sommet O.
Clairaut observe alors que l’on peut obtenir d’autres surfaces contenant la même courbe en combinant les équations des projections. Comme il se restreint aux équations polynômes, si P = 0 et Q = 0 sont des équations définissant une courbe, AP+BQ = 0, où A et B sont des polynômes quelconques, représente aussi une surface qui contient cette courbe. Si l’on part de deux surfaces quelconques, on peut trouver les équations des projections en éliminant une des variables x, y ou z. Et par ailleurs, écrit Clairaut, si on trouve une combinaison qui ne dépasse pas le premier degré en les trois variables, c’est l’équation d’un plan et la courbe n’est pas à proprement parler à double courbure : c’est une courbe plane. Ainsi, notre premier exemple avec P = y – x 2 et Q = z – x 2 donne lieu à la combinaison P – Q = y – z : la courbe est plane. La méthode est intéressante, mais n’est pas facile à mettre en œuvre, même avec seulement des polynômes.
De l’intérêt du calcul différentiel
Clairaut passe à une seconde partie : « Usage du calcul différentiel dans les courbes à double courbure ». Regardons comment il s’exprime : « On conçoit ici une courbe à double courbure AN comme composée d’une infinité de petits côtés Nn, de même qu’une courbe qui serait décrite sur un plan, ce qui fait que le prolongement d’un de ces petits côtés Nn est la tangente dans le point N ou n de cette courbe à double courbure. »
Il imite donc ce qui se fait pour les courbes planes. Avant de considérer son calcul, regardons comment est traitée la tangente à une courbe plane dans l’Analyse des infiniment petits pour l’intelligence des courbes, du Marquis de L’Hôpital (1661-1704). Cet ouvrage, publié en 1696, est un des tout premiers traités vulgarisant le calcul différentiel et c’est une des lectures de Clairaut. Pour étudier la tangente à la courbe plane AM, avec m sur la courbe, infiniment proche de M. La tangente sera donc la prolongation du segment [Mm], qui rencontre l’axe des x en T. Le but est de calculer la longueur PT, qu’on appelle la sous-tangente, voir la figure ci-dessous.
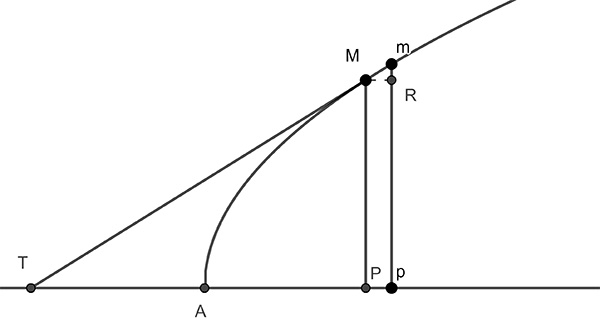
Le point p est la projection de m sur l’axe (AP) et la « petite droite » (MR) est parallèle à (AP), et l’on note AP = x, PM = y, donc Pp = MR = dx et Rm = dy. L’Hôpital observe que les triangles mRM et MPT sont semblables et il écrit :
C’est un peu obscur à nos yeux… Il faut connaître d’abord l’écriture a.b :: c.d. Elle représente une proportion, c’est-à-dire l’égalité
Cette notation est très fréquente et s’utilise encore au début du XIXe siècle. La démonstration s’écrirait donc, avec notre style moderne :
soit
d’où
C’est le résultat bien connu que le coefficient directeur de la tangente est le nombre dérivé
Pour expérimenter ce calcul, regardons le cas de la tangente à une parabole : M est d’abscisse x, d’ordonnée y = x 2.
On a donc dy = 2xdx et donc T est le milieu de [AP], propriété bien connue de la parabole.
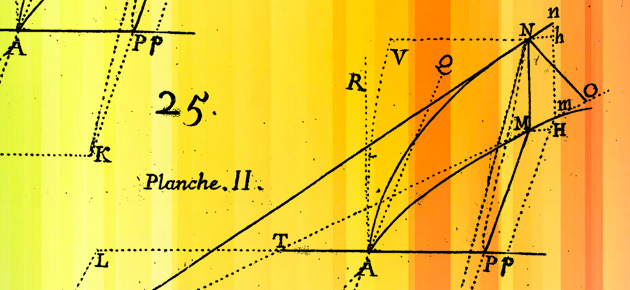
Clairaut va donc adapter cette démarche. On peut suivre son calcul en s’appuyant sur la figure suivante :
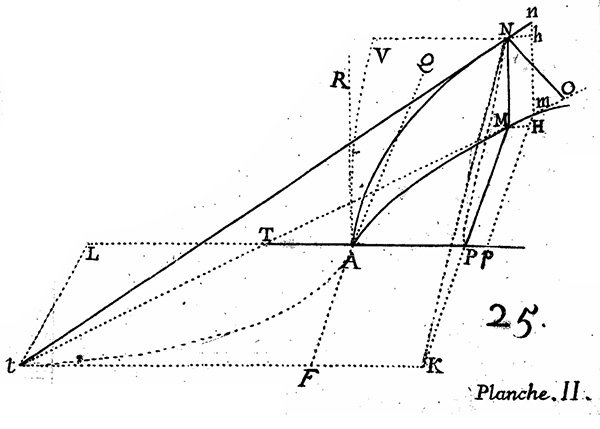
Extrait de Recherche sur les courbes à double courbure.
Une fois bien définis les points utiles, il écrit :
« Ainsi les triangles semblables nHh, Nmt donneront
qui fera valeur de la sous-tangente. »
La suite de la section contient divers autres calculs autour de la tangente, et Clairaut remarque que
ce qui permet d’exprimer la sous-tangente de la courbe à double courbure en fonction des sous-tangentes des projections sur les plans Oxz et Oyz d’où l’observation que la tangente à la courbe à double courbure se projette sur les tangentes des deux projections planes. Et il donne bien sûr des exemples. La suite de la section concerne les plans tangents aux surfaces, et la manière de les utiliser pour obtenir les tangentes d’une courbe à double courbure qui est l’intersection de deux surfaces. Clairaut s’intéresse aussi à la trace que laisse sur un plan de base la tangente à une courbe à double courbure.
La troisième section « Usage du calcul intégral dans les courbes à double courbure, par rapport à leurs rectifications et à la quadrature des espaces qu’elles déterminent, etc. » se consacre donc à des calculs de longueurs (rectification) ou d’aires (quadrature). Par des considérations de petits segments, Clairaut obtient que l’arc AN est
la lettre S désignant le symbole
d’intégration.
Suivent des exemples, un peu « truqués » pour que les intégrales puissent se calculer explicitement… Clairaut calcule aussi des aires (essentiellement celles de portions de cylindres) et propose des problèmes plus subtils, comme celui de déterminer l’équation de la courbe obtenue en dépliant un des cylindres contenant une courbe à double courbure. On trouve également de nombreux calculs de volumes.
Rappelons encore que ce livre est plaisant, élémentaire et qu’il faut le lire activement, refaire les calculs, faire les figures… Dans ce cas, pour dessiner les courbes gauches, il vaut mieux chercher une représentation paramétrique en sachant malgré tout que c’est un outil que Clairaut n’utilise pas.
Géodésiques et épicycloïdes
Clairaut, jeune académicien vedette, a rapidement été l’objet de la curiosité des mathématiciens européens. Notamment de celle de Johann Bernoulli, alors le plus connu et influent des successeurs de Leibniz. En 1731, il a soixante-quatre ans et a succédé à son frère et rival Jacob dans la chaire de mathématiques de l’université de Bâle ; il correspond avec de nombreux mathématiciens. Clairaut, qui a fait la connaissance du mathématicien suisse Gabriel Cramer (1704-1752), en visite à Paris, utilise l’intermédiaire de celui-ci pour lui faire parvenir son livre.
Dans une lettre à Cramer, Bernoulli écrit : « Quant au reste, M. Clairaut ferait bien de pousser plus loin les recherches sur les courbes à double courbure, car il n’ a fait encore qu’ effleurer cette matière, quoique ce soit beaucoup pour son âge, le plus difficile serait de déterminer des courbes sur une surface courbe donnée, qui fissent la fonction de quelque maximum ou minimum, p. ex. la courbe à double courbure de la plus vite descente, ou simplement celle qui soit la plus courte entre deux points sur une surface courbe donnée, ce que j’ai proposé il y a déjà de longues années et dont j’ai donné des solutions générales à M. de Maupertuis et Klingenstrein, quoique M. Clairaut dise dans la préface être le premier qui ait médité et traité cette matière. » (lettre à Cramer, 1er septembre 1731).

Johann Bernoulli (1667-1748).
Des éloges, mais aussi un défi. Il s’agit donc surtout de caractériser, pour une surface quelconque, la courbe la plus courte entre deux points A et B. C’est ce qu’on appelle une courbe géodésique. Le problème est connu depuis longtemps, et Bernoulli en a discuté avec son frère ennemi Jacob et avec Leibniz. La solution est simple dans certains cas comme les cylindres (il suffit de les déplier…) ou les sphères : le plus court chemin est alors un arc de grand cercle, intersection de la sphère de centre O avec le plan passant par O, A et B.
Clairaut ne répond pas tout de suite, Bernoulli le relance une fois, par l’intermédiaire de Cramer en mai 1732. Le jeune mathématicien lui envoie, en octobre, une première réponse, mais Bernoulli n’est pas totalement satisfait et il lui écrit le 2 novembre. Cela se conclura, pour Clairaut, par son mémoire Sur quelques questions de maximis et minimis, présenté à l’Académie des sciences en février 1733, mémoire qui élargit un peu le problème. La question des géodésiques ne s’arrête pas là : Bernoulli n’a pas proposé son problème au seul Clairaut, il a également sollicité son élève Leonhard Euler, lui aussi très jeune puisqu’il est né en 1707, six ans avant Clairaut. La solution d’Euler est publiée en 1732 à l’Académie de Saint-Pétersbourg, ville où il réside, dans un article en latin intitulé De linea brevissima in superficie quacunque duo quaelibet puncta jungente (« La ligne la plus courte sur une surface joignant deux points quelconques »). Ces premiers travaux sur ce thème seront poursuivis en d’autres occasions, donnant lieu, chez le mathématicien bâlois, aux prémices de ce qu’on appelle maintenant le calcul des variations.
Parallèlement, Clairaut va s’intéresser aux épicycloïdes sphériques (le mémoire Des épicycloïdes sphériques est présenté à l’Académie en 1732). Imaginons un cercle qui roule (on est dans l’espace) sur un autre cercle, incliné d’un angle constant. Un de ses points parcourt une épicycloïde sphérique. Bernoulli et Maupertuis participeront aussi à la recherche des épicycloïdes qui sont algébriquement rectifiables, c’est-à-dire dont la longueur s’exprime avec des expressions dénuées de fonctions transcendantes (trigonométriques, logarithmiques…). Tous les trois enverront leur solution presque en même temps à l’Académie des sciences.
Maupertuis est un ami de Clairaut. Il se rendra à Bâle avec lui pour rencontrer Johann Bernoulli à l’automne 1734 et ils participeront ensemble à l’expédition en Laponie en 1736.
Dans l’héritage mathématique de Clairaut, la géométrie tient une grande place. C’est essentiellement de la géométrie qui s’appuie sur le calcul différentiel, et elle est présente dans ses travaux fulgurants des premières années.

Tombeau de Petrus Ludovicus Moreau de Maupertuis, église Saint-Roch, Paris.
[encadre]
Les éléments de géométrie
Les Éléments de géométrie est un ouvrage de Clairaut, paru en 1741 (il sera suivi des Éléments d’algèbre ; voir en page 22), qui sera réimprimé et réédité pendant plusieurs dizaines d’années.
Destiné à l’enseignement, il est d’une grande originalité. Comme il le dit dans sa préface, Clairaut veut s’affranchir du modèle axiomatique d’Euclide, sans pour autant se limiter à un traité de géométrie pratique. On est prévenu : « On me reprochera peut-être de m’en rapporter trop au témoignage des yeux et de ne pas m’attacher à l’exactitude rigoureuse des démonstrations. »
Nous nous contenterons de regarder le début du traité. Après nous avoir convaincu que la distance entre deux points A et B est obtenue en reliant ces points par une ligne droite, Clairaut se pose la question d’évaluer la distance entre un point D et une droite (AB). Il écrit : « il est aisé de voir que c’est la ligne DC qu’on suppose ne pencher ni vers A, ni vers B. (…) à laquelle on a donné le nom de perpendiculaire… » Cela paraît très intuitif. Trop ?
Par la suite, Clairaut explique la construction de la perpendiculaire à la droite (AB ) élevée de C, milieu de [AB ] : « il faudra que cette ligne ne penche ni vers A, ni vers B. […] Il est clair que chacun des points D de cette ligne sera également éloigné de A et de B. Pour avoir le point D, on pourrait le chercher par tâtonnement, mais le tâtonnement ne satisfait pas l’esprit, il veut une méthode qui l’éclaire. »
On relève l’expression « il est clair que » qui annonce une absence de démonstration. Cependant Clairaut veut enseigner une géométrie pratique, et il donne ensuite la construction classique de la perpendiculaire (ici médiatrice de [AB ] ). On prend une « commune mesure », avec un compas, ou une corde si on est sur le terrain, et on trace deux arcs de même rayon de centre A puis de centre B, ils se coupent en un point D qui convient.
[/encadre]











