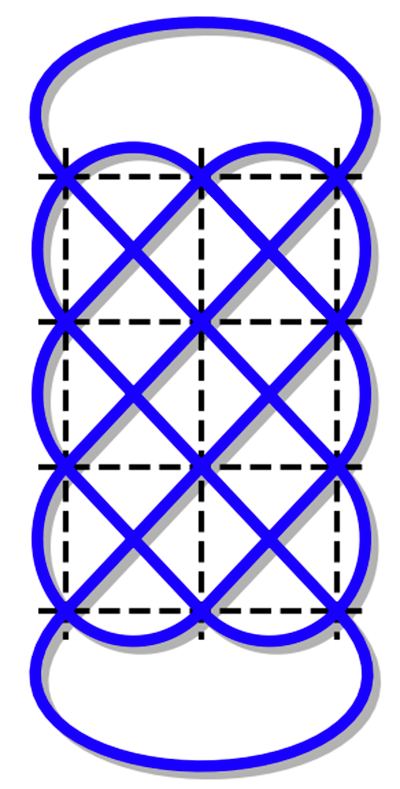
L’algorithme de la tortue

Nous voici au Vanuatu (anciennement Nouvelles-Hébrides), un archipel du Pacifique composé de 83 îles, et en particulier chez les Raga du nord de l’île de Pentecôte (carte ci-contre). On y pratique une activité nommée « dessin sur le sable » qui est une fenêtre ouverte sur le monde tel que le voient les Ragas.
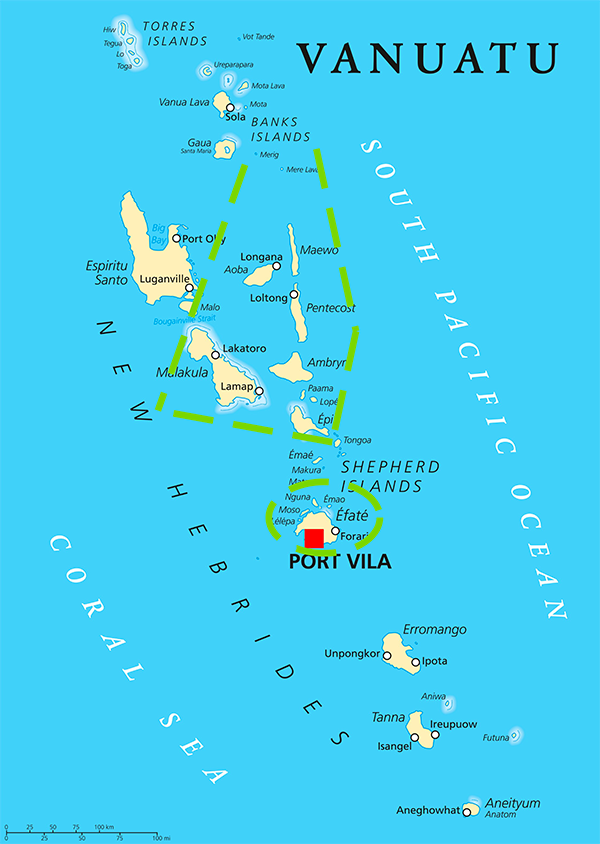
Les tirets verts indiquent les zones de pratique du dessin sur le sable.
Doté à ce jour d’une population d’environ 315 000 personnes, le Vanuatu possède la plus haute densité linguistique au monde, puisqu’on y dénombre 138 langues. Ce constat se traduit par des réalités culturelles différentes et, s’il existe des traits communs à toutes les sociétés du Vanuatu, nombre de variations culturelles permettent à chacune d’entre elles de se démarquer. Ainsi, nous parlerons plus loin du « dessin sur le sable du Vanuatu », mais il faut garder à l’esprit que cette pratique n’est répandue que dans les îles du centre. Bien que dans ces îles, cette pratique soit connue de tous et que les dessins les plus simples circulent librement, il n’existe qu’un petit nombre d’experts – des hommes et des femmes que nous nommerons praticiens – connaissant les dessins les plus ardus. Ce sont des personnes qui peuvent être de tous âges : de jeunes dessinateurs créant de nouveaux dessins ou des aînés reconnus pour leur connaissance encyclopédique de la pratique. Ajoutons que cet art éphémère – le dessin étant effacé une fois terminé – stimule la narration : les praticiens concluent généralement leurs dessins par le récit d’un mythe ou d’un conte. Il n’est pas rare qu’ils fassent alors appel à l’imagination des spectateurs, suggérant au sein du dessin des détails en lien avec leur histoire : des lieux, des personnages, des animaux…
La pratique obéit le plus souvent à un certain nombre de « règles » qu’il convient à présent d’énoncer. Le contexte du Vanuatu étant celui de la tradition orale, les « règles » ne font que rarement l’objet de discours particuliers de la part des praticiens. Par règle, on entendra donc plutôt « caractéristiques observées dans la majorité des cas ».


Le dessin Tutel (Centre culturel du Vanuatu, 2019).
Les « règles » de dessin
Le praticien commence par tracer une « grille » qui peut présenter de nombreuses formes et tailles : rectangles, assemblages de rectangles, cercles concentriques… L’analyse du vocabulaire vernaculaire montre que les grilles jouent un véritable rôle d’armature pour le dessinateur. D’ailleurs, le vocabulaire de la grille est emprunté à celui de la construction des imwas (cases traditionnelles, voir photographie ci-dessous).



Préparation du sol et tracé d’une grille rectangulaire, Pentecôte 2019.
Une fois la grille achevée, le praticien trace une ligne avec l’extrémité d’un doigt dont les caractéristiques sont le plus souvent les suivantes :
• La ligne est continue : le doigt ne se soulève pas du sol pendant la réalisation du dessin ;
• Le tracé n’intersecte la grille qu’en ses nœuds. Le tracé s’effectue donc d’un nœud de la grille à un autre ;
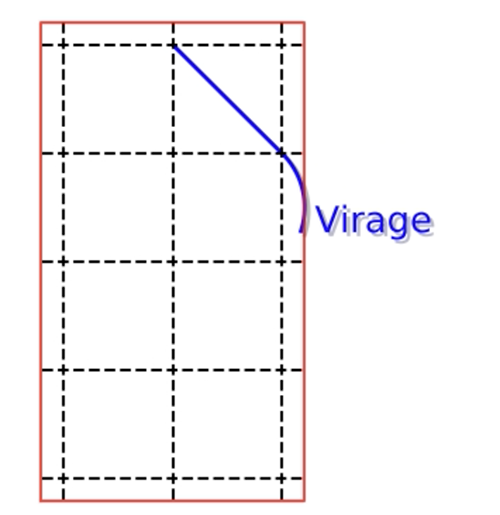
• En chacun de ces nœuds, le tracé s’appuie sur une des deux droites (voir ci-dessous). Lorsque le doigt traverse le nœud, il n’y a généralement pas de rupture de direction et donc pas de point anguleux ;
• Le dessinateur évite de repasser continûment sur une partie déjà existante. Il peut néanmoins créer des points de croisement. C’est notamment le cas des nœuds de la grille qui sont souvent traversés plusieurs fois ;
• Une fois le dessin terminé, l’index est revenu au point de départ, dans la même direction de départ ;
• La figure finale possède au moins un axe de symétrie.

Chaque nœud traversé par le doigt l’est selon une des deux directions rouges.
[encadre]
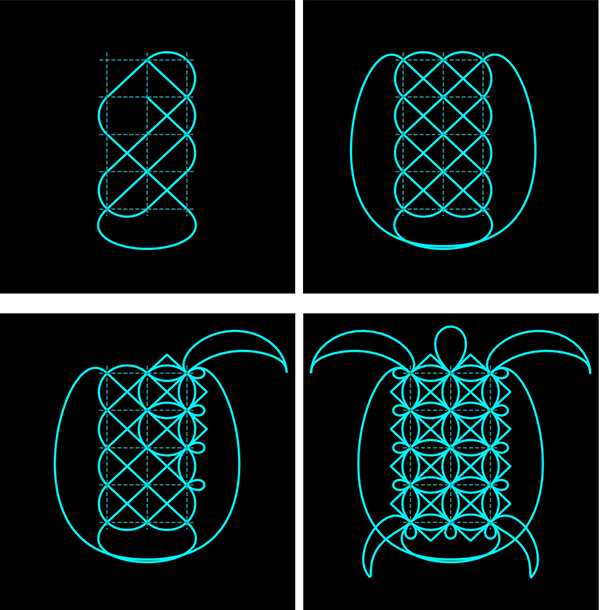
Quelques étapes de T (5, 3)
L’analogie avec le billard – au rôle joué par les coins près – permet de comprendre les étapes à réaliser.
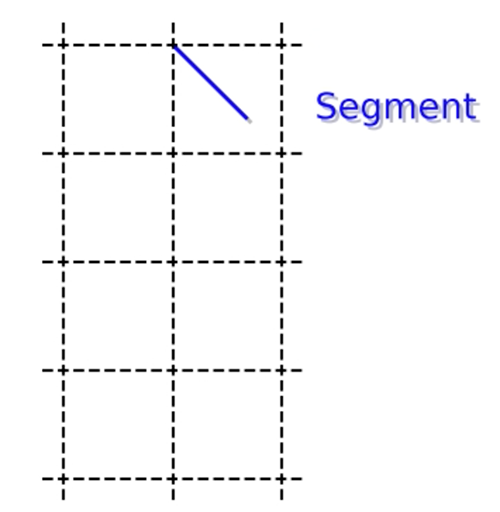
Déplacement en ligne droite.
Rebond sur un bord fictif.
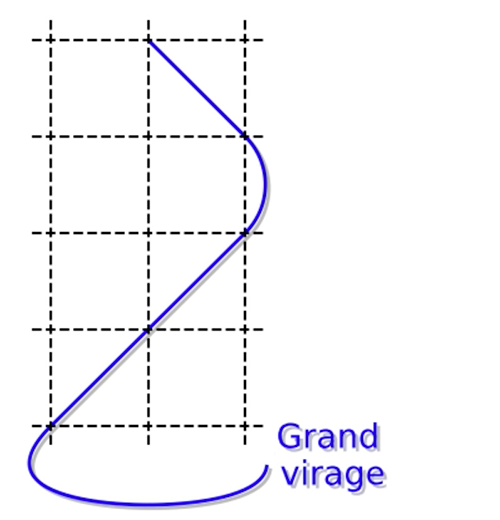
Il n’y a pas de rebond dans les coins, mais un grand virage
qui amène sur le coin opposé horizontalement.
Rebond sur le bord fictif en bas.
[/encadre]
Muni de ces « règles », nous pouvons désormais passer à la description d’une procédure de dessin, dont nous allons montrer qu’elle peut être considérée comme un algorithme dépendant de la taille de la grille.
L’algorithme de la tortue
Nous avons désigné par « algorithme de la tortue », une procédure de dessin exécutée au cours d’un dessin de tortue. Ce choix fait écho à un échange avec un praticien qui, ayant réalisé un dessin a expliqué le tracé de la « première partie » par une liste d’instructions : « tu traverses », « tu tournes » ou encore « tu reviens ». Cette forme narrative suggère que le praticien exécute la première partie de ce dessin comme une suite d’instructions conditionnées à la position du doigt dans le dessin et devant être exécutées jusqu’à revenir au point de départ. Il a été mis en évidence que cet algorithme était utilisé pour construire des dessins plus complexes sur des grilles de différentes tailles.
L’algorithme de la tortue, lorsqu’il est produit sur une grille à l lignes et c colonnes, sera donc noté T (l, c).
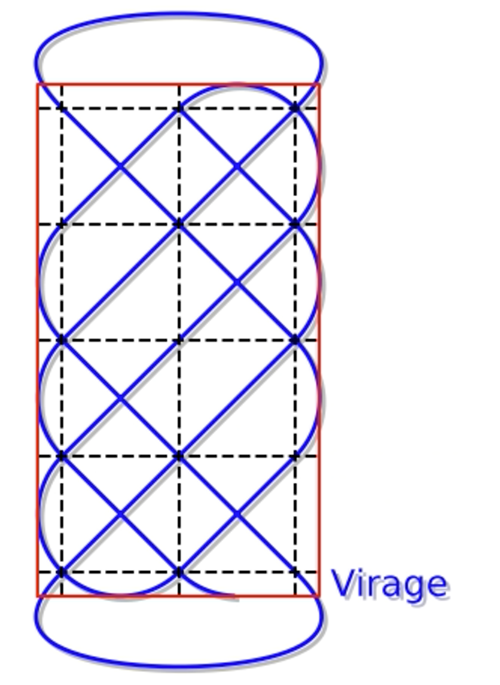
Pour expliquer cet algorithme, utilisons une analogie (suggérée, d’une certaine façon, par les commentaires évoqués précédemment). On peut imaginer que le tracé du doigt matérialise la trajectoire d’une boule se déplaçant en ligne droite à l’intérieur d’un billard rectangulaire fictif. Soyons clair : ce billard ne fait pas partie du dessin et n’a pas été indiqué par les praticiens. Le point de départ et la direction de départ sont au choix du dessinateur, même si les praticiens démarrent généralement d’un point du bord supérieur. Les figures ci-contre montrent quelques étapes de cet algorithme, exécuté sur une grille à 5 lignes et 3 colonnes, et démarrant du point supérieur central dans une direction à −45°. Les termes « segment », « virage » et « grand virage » désignent certains types de tracés entre deux points de la grille, ils permettent de comprendre le principe suivant :
• la boule se déplace librement en ligne droite dans le billard ;
• la boule change de direction lorsqu’elle rencontre le bord du billard (elle fait un « virage » ) en dehors des coins ;
• lors de ce changement de direction, l’angle d’incidence est égal à l’angle de réflexion ;
• si la boule rencontre un coin sortant, elle rentre dans le billard par le coin symétrique par rapport à l’axe de symétrie vertical.
[encadre]
Différents cas de l’algorithme de la tortue.
T (4, 3) – complet.
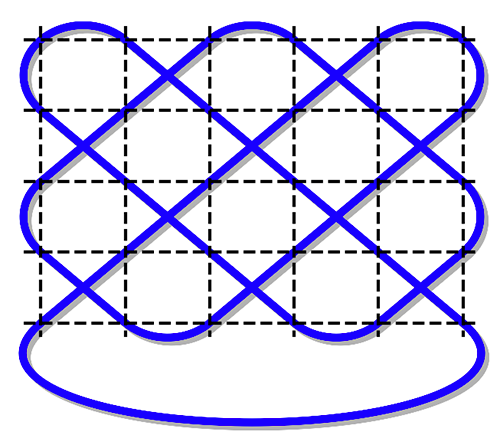
T (5, 6), c est pair – incomplet.
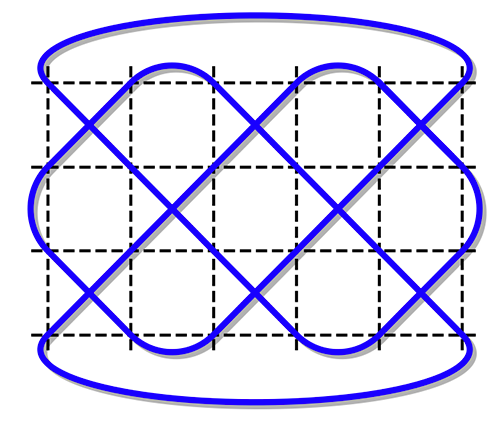
T (4, 6), c est pair et non premier avec l – incomplet.
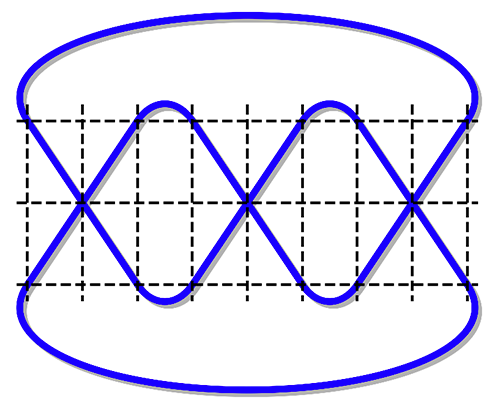
T (9, 3), l et c ne sont pas premiers entre eux – incomplet.
[/encadre]
Comme l’illustre la figure de l’encadré ci-dessus, on se rend en effet compte que, dans certains cas, l’algorithme ne semble pas compléter totalement la grille : certains nœuds ne sont soit pas traversés du tout (pour (l, c) = (9, 3) par exemple), ou alors seulement dans l’une des deux directions possibles (pour (l, c) = (4, 6) par exemple). Les experts placés dans ces situations font remarquer que le dessin n’est pas « complet » (compleat en bislama). Nous dirons donc que l’algorithme est « complet » si tous les nœuds de la grille sont traversés, et ce, dans les deux directions possibles. C’est par exemple le cas de la figure T (4, 3) (voir illustration ci-dessus).
Il a été démontré que l’algorithme T (l, c) est complet si et seulement si les deux conditions suivantes sont réalisées : c est impair et l et c sont premiers entre eux.
Muni de ce résultat, on a cherché à comprendre quel type de savoir en avaient les praticiens. En effet, dans tous les dessins où l’algorithme de la tortue est mobilisé au cours du tracé, les conditions du théorème sont réalisées. Les praticiens sont-ils capables de savoir spontanément si un couple (l, c) convient, ou bien connaissent-ils un certain nombre de valeurs pour lesquelles T (l, c) est complet ? De plus, quels discours tiennent-ils lorsque on les place dans des conditions dans lesquelles T (l, c) n’est pas complet ? Ces questions vont nous emmener sur l’île d’Ambrym.
Le cas du dessin Poar
Eric Vandendriessche, qui mène des recherches sur le nord de l’île d’Ambrym depuis plus de quinze ans, a remarqué l’intérêt d’un dessin nommé Poar, ce terme vernaculaire désignant une espèce d’oiseau marin. Ce dessin, généralement réalisé sur une grille de dimension (l, c) = (3, 5), représente cinq oiseaux posés dans une rigole pleine d’eau (figure ci-dessous). Il existe au Nord-Ambrym plusieurs façons de faire ce dessin, mais toutes ces méthodes possèdent un invariant. En effet, de façon assez inattendue, une des étapes de la construction peut toujours être interprétée comme la réalisation de l’algorithme de la tortue T (2, 5) sur les deux dernières lignes de la grille de ce dessin (voir illustration page suivante).
Partant de ce constat, il a été proposé aux praticiens maitrisant parfaitement ce dessin de réaliser le dessin Poar dans des configurations inhabituelles pour eux. On leur a ainsi demandé de réaliser le dessin sur des grilles de taille (3, c), c ≥ 3. Le dessin nécessite alors de réaliser l’algorithme T (2, c), pour lequel le théorème de la tortue indique qu’il faut choisir c impair. Les résultats de cette expérimentation se sont révélés fructueux. Tout d’abord, les praticiens ont mentionné spontanément qu’il était nécessaire de choisir un nombre de colonnes impair. Ensuite, ils se sont adaptés à la nouvelle taille de grille et ont réalisé spontanément le dessin dans les cas c = 7, 9, 11… (figure ci-dessous).


Deux versions du dessin Poar.
Pour la figure du haut : l = 3, c = 5 et pour la figure du bas : l = 3, c = 11.
Ceci amène deux commentaires. D’une part c’est une indication forte que la procédure est bien perçue par les acteurs comme un algorithme dont les instances sont le nombre de lignes et de colonnes. D’autre part, même s’ils ne semblaient pas entrevoir de liens avec le dessin Tutel, ceci semble bien confirmer que l’algorithme de la tortue ait pu circuler d’une île à l’autre et constituer une base à la création de différents dessins.
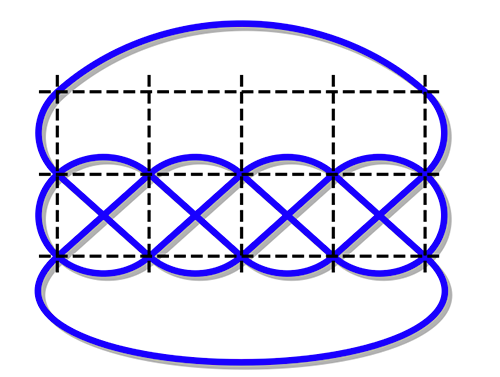
Une des étapes du dessin Poar sur grille (3, 5) peut être identifiée
comme la réalisation de T(2, 5) sur la partie basse de la grille.
Ces résultats donnent un bref aperçu de la façon dont on peut interroger la nature mathématique du dessin sur le sable. Ce sont de nouveaux outils pour l’ethnographe. L’identification des valeurs du couple (l, c) qui rendent T (l, c) complet permet en effet d’interagir avec les praticiens avec une meilleure connaissance de la pratique. D’une façon plus générale, tous les outils mathématiques et informatiques développés ne l’ont été que pour comprendre le point de vue des praticiens et notamment d’interroger la façon dont les dessins sont crées, mémorisés et transmis.
L’algorithme T (l, c) n’est utilisé que dans le cadre de dessins relatifs au monde animal : tortues, oiseaux, vers, sauterelles ou encore papillons. Ceci permet d’ouvrir la voie à une question plus anthropologique : « En quelle(s) mesure(s) cet algorithme est-il révélateur des liens qu’entretiennent ces sociétés avec le monde animal ? ».

Un des deux praticiens executant un dessin dont T (19, 7) constitue la base.
Le travail sur les aspects ethnomathématiques du dessin sur le sable semble loin d’être terminé. On a, par exemple, récemment identifié au sein d’un dessin, l’algorithme T (19, 7) (figure ci-dessous) ! La grille étant imposante, deux praticiens se relaient pour tracer la ligne continue, ce qui implique que l’un et l’autre connaissent le même algorithme et que l’un suit l’évolution de l’autre lorsqu’il est inactif. Comment ont-ils su que les valeurs numériques l = 19 et c = 7 convenaient ? On n’a pas de réponse à ce jour. Preuve qu’il reste encore beaucoup à faire sur le sujet !

T (19, 7) ayant subi une rotation de 90° constitue la base d’un dessin à deux mains.