Les abeilles : un réel sens abstrait du nombre

By

Les mathématiques sont certainement l’un des exemples les plus frappants de la discontinuité cognitive entre les humains et les autres animaux. En effet, qu’il y a-t-il de plus abstrait que la manipulation de symboles mathématiques ? Cependant, les capacités de raisonnement mathématique, bien qu’elles s’acquièrent au travers de l’éducation par transmission culturelle, reposent néanmoins sur un ensemble de compétences mathématiques préscolaires d’origine biologique, partagées entre autres par les primates non humains. En effet, les chimpanzés peuvent dénombrer et ordonner de petites quantités, résoudre des problèmes arithmétiques simples sur la base d’additions et de soustractions et associer des symboles tels que les chiffres arabes à des quantités. Ces facultés pourraient donc être considérées comme les racines biologiques de nos mathématiques.

Étant donné la grande valeur adaptative d’une capacité à dénombrer dans des situations aussi diverses que pour choisir une quantité de nourriture, évaluer les rapports de forces entre groupes sociaux selon leur taille ou encore aider à se repérer dans l’environnement ou à reconnaître des objets, il n’est peut-être pas surprenant de retrouver cette capacité chez de nombreuses espèces de vertébrés, des poissons aux mammifères en passant par les oiseaux. Seuls les reptiles en semblent dépourvus. Il est vrai qu’en proportion de leur taille, leur cerveau est plutôt petit mais il faut reconnaître qu’il n’est pas évident pour les chercheurs de motiver un serpent ou un crocodile à lui montrer ses capacités intellectuelles ! Par contre, apprendre que même des insectes peuvent évaluer des quantités surprendra peut-être plus, ne serait-ce que de par leur cerveau miniature (eh oui, les insectes ont bien un cerveau !) mais aussi, bien sûr, par leur distance évolutive à l’humain. Or certaines espèces de fourmis peuvent compter leur nombre de pas pour évaluer les distances ou se baser sur un nombre de repères visuels ; elles se montrent aussi plus agressives si elles sont dans un groupe de taille plus importante en cas de conflit. Les vers de farine sont attirés par un substrat avec l’odeur d’un plus grand nombre de femelles, les bourdons peuvent évaluer un niveau de compétition suivant le nombre d’autres bourdons visitant une source de nourriture ou les grillons plus facilement s’enfuir vers une zone avec le plus grand nombre d’abris potentiels. Au-delà des insectes, des araignées sont aussi capables de mémoriser le nombre de proies prises dans leur toile ou les seiches choisir de chasser le banc avec le plus grand nombre de crevettes.

L’intérêt d’étudier les abeilles

Mais est-ce que ces exemples sont vraiment des preuves d’un « sens du nombre », c’est-à-dire la capacité à reconnaître une quantité précise d’objets et ce, indépendamment d’autres paramètres physiques qui sont liés aux quantités comme la densité, la surface cumulée ou la quantité de mouvement ? Pour vérifier l’existence d’un réel sens abstrait du nombre, tel que le nôtre, il est nécessaire de passer par des procédures expérimentales contrôlées. Les capacités des abeilles ont ainsi été particulièrement étudiées ces dernières années. Pourquoi les abeilles ? Pour trois raisons principales.

Premièrement, le comportement de butinage des abeilles requiert de bonnes capacités d’apprentissage, ce qui en fait un modèle idéal pour étudier toutes formes d’intelligence. En effet, les abeilles doivent être capables d’apprendre à reconnaître les fleurs d’intérêt parmi toutes les options disponibles, de mémoriser l’endroit où les retrouver et le moment de la journée où elles fournissent du nectar, mais aussi de se repérer dans l’environnement car retrouver sa ruche, située souvent à plusieurs kilomètres des fleurs exploitées, revient à trouver une aiguille dans une botte de foin !

Deuxièmement, les abeilles sont très coopératives avec les chercheurs ! Non seulement il est très facile d’avoir des milliers d’abeilles à disposition à proximité du laboratoire mais, peu peureuses, elles sont volontaires pour venir participer aux expériences en échange d’un peu d’eau sucrée, équivalent au nectar collecté par les butineuses. Ainsi, elles font toute la journée des allers-retours toutes les trois minutes entre la ruche et notre dispositif expérimental, nous permettant de collecter de nombreuses données.

Troisièmement, et c’est en grande partie la conséquence des deux premiers points, les abeilles sont étudiées depuis des dizaines d’années par de nombreuses équipes de recherche dans le monde afin de mieux connaître leur perception, leur comportement et leurs capacités cognitives (voir encadré). Ainsi, on peut construire des protocoles expérimentaux complexes en se reposant sur les connaissances acquises sur ce qu’elles sont capables de percevoir et d’apprendre, mais aussi sur les méthodes les plus efficaces pour travailler avec elles. C’est ainsi que l’abeille est devenue un modèle clé en cognition animale.

[encadre]

La communication des abeilles

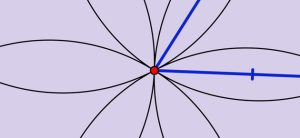
L’éthologue autrichien Karl von Frisch (1886-1982) est le premier à comprendre que les abeilles peuvent communiquer entre elles une véritable cartographie de leurs explorations à l’aide de danses indiquant des distances et des angles. La théorie mathématique utilise d’ailleurs cette méthode de coordonnées dans bien des problèmes géométriques : au lieu d’utiliser des coordonnées (x, y) cartésiennes indiquant l’abscisse et l’ordonnée, on préfère souvent des coordonnées polaires (ρ, θ) indiquant le rayon (c’est-à-dire la distance) et l’angle. Ainsi, une abeille, lorsqu’elle fait une danse pour indiquer un lieu, spécifie la distance au lieu décrit et l’angle que la ligne droite menant au lieu fait avec le soleil.

Von Frisch identifie ces danses lorsqu’il observe les abeilles qui partent à la recherche de nourriture : une abeille parcourt d’abord au hasard les environs de la ruche. Lorsqu’elle trouve de la nourriture, elle en mange un peu puis retourne dans la ruche. Elle régurgite alors de son estomac la nourriture qu’elle vient de recueillir. Aussitôt, deux ou trois autres abeilles, dont le rôle est de distribuer le miel, mangent ce qui vient d’être régurgité soit pour le donner à des abeilles affamées soit pour le placer dans les alvéoles. Pendant la distribution, la première abeille, celle qui est revenue chargée de nourriture, se met à danser : plus elle estime que la nourriture rapportée par elle est de bonne qualité, plus elle répète sa danse. Autour d’elle, quelques abeilles suivent le mouvement de sa danse, ce qui leur permet de savoir où aller chercher la nourriture à leur tour.

La longueur de la partie centrale où l’abeille frétille indique la distance à parcourir. L’angle de la danse reproduit l’angle au soleil du lieu.

[/encadre]

Des abeilles et des nombres

Alors, que sait-on des capacités des abeilles avec les nombres ? Tout d’abord, qu’elles savent compter sans erreur jusqu’à 5 en ordonnant les chiffres du plus petit au plus grand en incluant le zéro. La limite de 5 parait bien basse mais sachez que nous ne sommes pas meilleurs si on doit reconnaître des quantités sans pouvoir recourir à la comptine numérique (un, deux, trois…). Cette limite semble d’ailleurs universelle, posant des questions fascinantes sur l’évolution du sens du nombre (voir encadré). Plusieurs méthodes ont été utilisées pour arriver à cette conclusion : tout d’abord, dès les années 1990, une équipe de recherche allemande a entraîné des abeilles à faire des allers-retours entre la ruche et un pot rempli d’une solution sucrée. En chemin, les abeilles croisaient des tentes, placées en ligne entre la ruche et la récompense sucrée, à des distances variables sur une zone de quelques centaines de mètres au cours de la journée. Cependant, les abeilles pouvaient apprendre que la récompense était toujours placée après la troisième tente, par exemple (ou une autre position, selon les expériences). Après plusieurs heures d’entraînement, les chercheurs ont enlevé la récompense, déplacé de nouveau les tentes à des positions non utilisées lors de l’entraînement et ont alors constaté qu’un bon tiers des abeilles cherchaient la récompense après le bon nombre de tentes. Il a ensuite fallu attendre 2008 pour qu’une équipe australienne reprenne cette question et confirme ce résultat mais dans des conditions plus contrôlées : cette fois-ci, les abeilles apprenaient à rentrer dans un tunnel étroit long de quatre mètres avec un couvercle transparent mais empêchant d’utiliser des repères visuels extérieurs. Elles trouvaient une récompense, là encore après un nombre fixe de repères (des bandes noires sur les murs du tunnel) dont la position exacte dans le tunnel variait au cours du temps. Cette fois-ci, la majorité des abeilles ont cherché après le bon nombre de repères lorsqu’on leur a enlevé la récompense. Elles continuent cette stratégie de recherche même si on change la forme, la couleur ou encore la taille des repères, suggérant un réel dénombrement. L’année suivante, leurs collègues ont testé une nouvelle façon de vérifier si les abeilles pouvaient compter : les abeilles étaient maintenant entraînées avec des labyrinthes en forme de « Y ». L’abeille faisait face à une image avec un certain nombre de symboles (formes géométriques) sur la porte du labyrinthe, puis avait ensuite le choix entre le bras gauche ou le droit dans lesquels étaient affichées d’autres images avec des symboles différents dont la taille, la disposition, la couleur, etc., variaient. Dans l’un des bras, l’image contenait le même nombre de symboles que l’image présentée à l’entrée mais pas dans l’autre. Si l’abeille choisissait le « bon » bras du labyrinthe, elle pouvait accéder à une récompense sucrée. Ainsi, par essai-erreur, au fur et à mesure des essais, les abeilles ont réussi à comprendre la règle du jeu leur permettant de récolter le sucre à tous les coups ! Elles réussissaient très bien cette tâche avec des petits nombres (de 1 à 4) puis commençaient à accumuler des erreurs plus les nombres augmentaient.

Il y a une dizaine d’années, l’autrice du présent article et son équipe ont repris le flambeau en collaboration avec une autre équipe australienne. Ils ont d’abord voulu vérifier si les abeilles comprenaient bien les nombres comme les humains, c’est-à-dire comme étant répartis de façon linéaire sur une ligne mentale, du plus petit au plus grand. Pour cela, l’équipe proposait aux abeilles des choix entre des images possédant deux quantités différentes de symboles (voir figure). Pour certaines abeilles, la règle à comprendre pour obtenir la récompense était de toujours choisir la plus petite quantité (et vice-versa pour d’autres abeilles). Bien sûr, les quantités, les symboles, leurs positions et tout autre paramètre variaient d’un essai à l’autre et un même nombre pouvait parfois être récompensé et parfois non selon le nombre alternatif présenté simultanément. Les abeilles ont facilement compris cette tâche avec un très bon taux de réussite en moins de deux heures d’entraînement. Elles pouvaient donc comprendre la règle « plus petit que » appliquée aux nombres. Pour vérifier que la durée de l’entraînement ne leur permettait pas, tout simplement, d’apprendre la bonne réponse pour chacune des paires de quantités possibles (par exemple 2 vs 3 ou 1 vs 4), certaines paires n’ont été montrées aux abeilles que lors du test final pour confirmer qu’elles avaient bien compris la règle.

Les chercheurs ont même tenté, par curiosité, d’ajouter un dernier test final avec une image présentant 2 symboles et une image « vide », toute blanche. Qu’allaient faire les abeilles ? Choisir le 2 qui avait été récompensé bien souvent pendant l’entraînement ou extrapoler la règle pour choisir le « zéro » malgré l’étrangeté de cette nouvelle image toute blanche. C’est bien la seconde option qui a été choisie par la majorité des abeilles, montrant que leur sens du nombre s’étend ainsi jusqu’au zéro, ce qui est loin d’être évident chez les primates !

Photographie d’un dispositif utilisé pour étudier les capacités mathématiques des abeilles. Des abeilles identifiées individuellement par un point de peinture sont entraînées à choisir l’image présentant un nombre donné d’objets pour obtenir une goutte d’eau sucrée, voire choisir le plus petit ou le plus grand nombre démontrant ainsi une représentation ordonnée des quantités.

Après cette découverte, l’équipe a continué à explorer les capacités mathématiques des abeilles et montré qu’elles pouvaient catégoriser les nombres pairs et impairs ou associer des symboles abstraits à des nombres. Enfin, voulant explorer leur capacité à effectuer des opérations, l’équipe leur a proposé le protocole suivant, assez complexe mais résolu là aussi, avec une grande facilité par les abeilles : le dispositif du labyrinthe en « Y » a été repris avec une image d’entrée présentant un nombre donné de symboles et un choix à faire entre deux images avec des nombres différents de symboles dans chacun des bras du labyrinthe. La règle était la suivante : si les symboles à l’entrée sont jaunes, alors il faut choisir le bras avec le nombre présenté à l’entrée + 1 ; s’ils sont bleus, alors il faut choisir le bras avec ce nombre – 1… Bien que très élémentaires, nous sommes en présence d’opérations arithmétiques avec, en plus, acquisition d’un opérateur additif ou soustractif (représenté ici par la couleur).

Interroger l’abstraction

Toutes ces compétences nous rapprochent donc des capacités mathématiques des primates, voire des jeunes enfants de moins de 3 ans, et nous interrogent sur l’utilité d’une représentation abstraite des nombres. Une hypothèse privilégiée serait l’utilité potentielle forte de posséder des concepts tels que celui des nombres pour pouvoir se construire une carte mentale de son environnement facilitant ainsi la navigation. Mais il est aussi possible que cette compétence soit en fait relativement courante. En effet, même si l’abeille a quand même un million de neurones, cela reste très peu – 100 000 fois moins que les humains –, ce qui suggère des mécanismes sous-jacents peu gourmands en termes de ressources computationnelles et qui pourraient donc être quasi universels malgré le niveau d’abstraction requis. Les insectes sont peut-être ainsi la meilleure façon de pouvoir répondre à la question de l’universalité du langage mathématique. Depuis des siècles, des générations de scientifiques ont développé les mathématiques reposant sur des règles générales et abstraites pouvant être combinées pour décrire tout objet physique ou conceptuel. Mais serait-il possible d’imaginer un système totalement différent qui remplirait la même fonction descriptive des règles physiques de notre univers ? Un tel débat restera probablement philosophique, du moins jusqu’à ce que nous rencontrions un organisme extraterrestre intelligent ! Cependant, l’éloignement évolutif et donc perceptif et physiologique des insectes en fait certainement des organismes que l’on peut considérer d’une histoire évolutive indépendante en termes de cognition, nous donnant ainsi accès à un système de pensée alternatif, même s’il repose aussi sur un cerveau composé de neurones.

Dans tous les cas, ces découvertes sont une pierre supplémentaire dans le processus en cours de reconstruction de notre vision de la place de l’intelligence dans le monde vivant. La recherche actuelle nous pousse à une véritable remise en cause philosophique en reconsidérant la richesse cognitive dont peuvent faire preuve des insectes, montrant des signes d’empathie, d’émotion, des capacités de reconnaissance individuelles, un sens du jeu ou encore l’utilisation d’outils, même s’il reste encore bien du chemin avant de pouvoir réellement caractériser le degré de similarité avec les équivalents humains et le niveau de conscience de ces animaux. À tout le moins, ces nouvelles connaissances nous invitent à l’humilité et à la curiosité vis-à-vis de la vie qui nous entoure.

[encadre]

Évolution du sens du nombre

La capacité à reconnaître et utiliser des nombres abstraits est largement répartie au sein du règne animal. Il est intéressant de noter que la plupart des études montrent des similitudes dans les mécanismes sous-jacents. Par exemple, l’existence de deux systèmes de traitement des quantités semble conservée : un système rapide et précis pour les quantités jusqu’à quatre éléments et un système approximatif pour les quantités plus importantes. Tous les animaux testés, incluant les humains, possèdent aussi une représentation mentale linéaire des nombres avec les plus petits nombres à gauche. De plus, les primates possèdent des neurones spécifiques qui augmentent leur activité en réponse à des quantités données. Des neurones aux propriétés très similaires et dans des régions cérébrales homologues ont également été trouvés dans le cerveau de corvidés, de poussins ou de chats. De telles similitudes dans le traitement des nombres entre espèces éloignées suggèrent que les compétences mathématiques des vertébrés pourraient être héritées d’un ancêtre commun. Alternativement, nous ferions face à une évolution indépendante, mais convergente, potentiellement liée à l’émergence d’autres fonctions cognitives nécessitant l’abstraction, comme la navigation ou la communication référentielle, ou tout simplement, car les mêmes mécanismes optimaux pour traiter les quantités avec un cerveau composé de neurones auraient émergé indépendamment. La question de l’origine de la cognition mathématique fait donc toujours l’objet d’un débat animé. Les recherches chez les invertébrés peuvent ainsi apporter un regard extérieur avec un accès à une histoire évolutive totalement indépendante en termes de fonctions cognitives permettant d’explorer les moteurs de l’apparition des différentes formes d’intelligence. Nos recherches actuelles visent ainsi principalement à essayer de comprendre les mécanismes neurobiologiques de ce sens du nombre chez les insectes dans une perspective comparative ainsi que de tenter d’identifier, en comparant les compétences de différentes espèces d’insectes, les conditions favorables (socialité, navigation, reconnaissance fine,…?) à l’émergence d’un sens du nombre sophistiqué.

[/encadre]

Aurore Avarguès-Weber est directrice de recherche CNRS et chercheuse au Centre de recherches sur la cognition animale de l’université de Toulouse.