Quatre tours de mathémagie

Pour Martin Gardner, le lien entre mathématiques et magie est essentiel, car il démontre comment des concepts abstraits peuvent se traduire en une expérience magique pour le spectateur. Infatigable chercheur de magie, il s’intéresse aussi bien à l’étude des grands classiques qu’à la création de nouveaux tours, notamment pour leur intérêt mathématique : ils illustrent comment des principes simples peuvent engendrer des effets puissants. Dans son livre Mathématiques, magie et mystère paru en 1956, Martin Gardner explore le célèbre « tour des 27 cartes », un véritable pilier de l’histoire de la magie des cartes. Ce tour, considéré comme un classique intemporel, doit sa renommée à sa simplicité apparente et à sa profondeur mathématique. Gardner le considère comme « l’un des tours les plus intéressants qui soient ». Utilisant un principe ingénieux de tri et de distribution, il permet de deviner une carte choisie par le spectateur avec une précision déconcertante. Ce caractère universel en fait un point de passage obligé pour les magiciens et les passionnés de logique.
Le tour des 27 cartes
Voici comment fonctionne le tour. Le magicien montre au spectateur un paquet de 27 cartes différentes ; le spectateur en choisit une et la mémorise, sans en révéler l’identité. Par ailleurs, le spectateur est invité à choisir un nombre n entre 1 et 27. Le magicien mélange les cartes puis les distribue en trois piles, comme s’il les distribuait à trois joueurs, à ceci près que les cartes sont face apparente. Le spectateur indique ensuite dans quelle pile se trouve sa carte. Le magicien reprend toutes les cartes et répète l’opération deux fois encore : distribution en trois piles et indication du paquet contenant la carte. Le magicien reforme enfin le tas de 27 cartes, puis égrène les cartes jusqu’à la nième, qui s’avère être la carte que le spectateur avait choisie.

Les tours de cartes par Jean Siméon Chardin, vers 1735.
Pour comprendre comment cela fonctionne, quelques explications mathématiques sont nécessaires. Tout nombre entier peut être écrit de manière unique comme une somme pondérée des puissances de 3. Ainsi, chaque nombre entier de 0 à 26 peut s’écrire de cette manière : n = a2 × 32 + a1 × 31 + a0 × 30, avec a i ∈ {0,1,2}.
Par exemple, n = 12 = 1 × 32 + 1 × 31 + 0 × 30.
Son écriture en base 3 est donc 110.
De même, 19 = 2 × 32 + 0 × 31 + 1 × 30.
Son écriture en base 3 est 201.
Pour réaliser le tour, on numérote les positions des cartes de 0 à 26. Ainsi, la première carte a la position 0, la deuxième la position 1, et ainsi de suite jusqu’à la 27 e, qui a la position 26.
Lorsque l’on distribue 27 cartes en trois piles, chaque pile contient exactement 9 cartes. Intéressons-nous au voyage de 9 cartes situées au milieu du paquet complet des 27 cartes. Ce sont les cartes J à R dans le tableau ci-contre (chaque carte est associée à une lettre de l’alphabet, la 27 e correspondant au symbole %). La deuxième colonne présente la reconstitution du paquet (le paquet de gauche est en haut).
| Avant le mélange | Après la distribution en 3 piles |
Rang des cartes en base 3 |
| A | A | |
| B | D | |
| C | G | |
| D | J | 010 |
| E | M | 011 |
| F | P | 012 |
| G | S | |
| H | V | |
| I | Y | |
| J | B | |
| K | E | |
| L | H | |
| M | K | 110 |
| N | N | 111 |
| O | Q | 112 |
| P | T | |
| Q | W | |
| R | Z | |
| S | C | |
| T | F | |
| U | I | |
| V | L | 210 |
| W | O | 211 |
| X | R | 212 |
| Y | U | |
| Z | X | |
| % | % |
Après reconstitution du paquet, les cartes placées au centre ont toutes un point commun : ce sont les cartes dont le rang en base 3 est de la forme x1y. Cela veut dire que faire ce type de mélange, c’est obtenir la décomposition ternaire. C’est la clé de ce tour. Répéter ce processus deux autres fois permet de déterminer les deux autres poids x et y. Pour cela, il faut respecter une règle d’assemblage bien précise en fonction du nombre n = a2 × 32 + a1 × 31 + a0 × 30 choisi initialement par le spectateur et qu’il faut donc avoir décomposé. Au premier tour, on regarde la valeur de a0 (au second tour a1 et enfin a2) :
• Si a0 = 0, on place la pile contenant la carte du spectateur au-dessus des deux autres piles ;
• Si a0 = 1, on place la pile entre les deux autres ;
• Si a0 = 2, on place la pile en dessous.
On procède de même pour les deux réassemblages suivants. Ainsi, après trois distributions, le placement des piles détermine les trois poids qui représentent la position de la carte choisie.
Par exemple, si le spectateur a énoncé le nombre 18 lorsqu’il lui a été demandé de choisir un nombre, on doit tout d’abord décaler d’une position pour obtenir 17 (puisqu’on numérote de 0 à 26 alors que le spectateur numérote de 1 à 27) puis décomposer ce nombre : 17 = 1 × 32 + 2 × 31 + 2 × 30 soit 122 en base 3. Au premier tour, la pile contenant la carte doit être placée au-dessous (a0 = 2) ; au deuxième tour, la pile doit être placée également au-dessous (a1 = 2) ; puis au milieu (a2 = 1).
Quelques petits conseils pour ne pas se tromper :
• Il faut avoir le paquet de 27 cartes en main, les cartes faces en bas.
• La distribution se fait de gauche à droite, carte par carte.
• Les cartes sont distribuées face en l’air.
• Lorsque le spectateur désigne le paquet où figure sa carte, les trois piles sont retournées face en bas.
On remarque enfin que l’on peut simplifier le tour en demandant au spectateur de choisir uniquement la carte, mais pas le nombre entre 1 et 27. En ce cas, on peut par exemple systématiquement mettre au milieu la pile contenant la carte du spectateur et alors sa carte apparaîtra en 14e position. En effet, placer trois fois la pile contenant la carte au milieu correspond à trois poids égaux à 1, donc au nombre ternaire 111, qui vaut 1 × 32 + 1 × 31 + 1 × 30 = 13. Il faut rajouter une unité pour retrouver l’échelle du spectateur (de 1 à 27 et non de 0 à 26), ce qui fait que sa carte sera toujours la 14e.
Un, deux, trois
Outre les tours préexistants qu’il a étudiés, Martin Gardner en a inventé beaucoup qui sont assez simples à réaliser. En voici un premier.
Le magicien présente trois tasses de couleur différente et remet au spectateur trois boulettes de papier de même couleur que les tasses. Le spectateur doit les placer sur les tasses en respectant cette consigne : la boulette doit être d’une couleur différente de la tasse. Ci-contre une configuration possible (1).
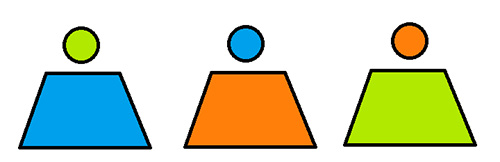
configuration 1
Le magicien explique qu’il savait que le spectateur allait faire ce choix. Il soulève chacune des tasses et on découvre qu’il y a trois boulettes sous chaque tasse dont la couleur coïncide avec celle du spectateur (configuration 2).
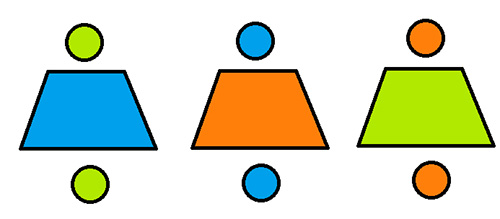
configuration 2
Voici comment le tour fonctionne. Tout d’abord, il faut préparer le terrain en plaçant au préalable les boulettes sous les tasses comme dans le dessin ci-contre. Il y a deux cas à considérer.
Cas n° 1 : le spectateur place les boulettes comme dans la description. Le magicien n’a plus qu’à soulever les trois tasses.
Cas n° 2 : le spectateur place les boulettes de la manière suivante (configuration 3).
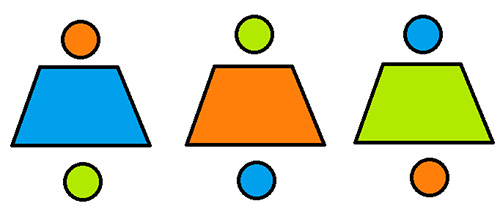
configuration 3
Le magicien explique avoir influencé les choix par le principe « arc-en-ciel ». Il soulève alors les tasses et fait remarquer qu’à chaque fois les couleurs sont différentes : arc-en-ciel ! Pour finir, il prend la tasse coiffée de la boulette orange, la retourne et révèle une pastille orange (préalablement collée au fond de celle-ci). La coïncidence s’étend aux autres tasses.
Le joueur surpris
Il s’agit cette fois d’une démonstration de tricherie. La préparation est très simple : les quatre as sont, au préalable, placés sur le dessus du paquet et c’est prêt !
Le magicien indique aux spectateurs qu’il existe une manière de tricher qui consiste à distribuer les cartes à partir du dessous du jeu plutôt qu’à partir du dessus. Cette technique permet d’obtenir un excellent jeu au poker. Il retire les quatre rois, les montre clairement au public et les place sous le paquet. Il distribue ensuite cinq mains de poker et, à chaque fois qu’il se donne une carte, il la prend ostensiblement au-dessous du paquet. Une fois les cinq mains distribuées, il révèle son jeu : un carré de rois ! Il replace alors les cinq mains, sans en altérer l’ordre, sur le paquet et explique qu’avec les techniques modernes, les cartes importantes sont plutôt sur le dessus du jeu. Puis il distribue normalement cinq mains de poker (la dernière main distribuée est pour lui) et explique qu’il va à nouveau se donner le carré de rois. Une fois la distribution terminée, il retourne ses cartes et dévoile… un carré d’as. Il conclut : « Un vrai tricheur ne dévoile jamais ses secrets, mais disons qu’avec un carré d’as, j’ai de bonnes chances de gagner ! »
[encadre]
Fibonacci revisité
Pour ce tour de Martin Gardner, nous allons partir d’une découverte d’un autre magicien : Stewart James, concernant les suites de Fibonacci. Rappelons que ces suites commencent par deux nombres quelconques et que chaque nouveau nombre est la somme des deux derniers nombres de la série. Ainsi, en partant de 5 et 7, on génère la suite de nombres 5, 7, 12, 19, 31 …
Précisons à présent la notion de racine numérique d’un nombre : il s’agit de l’addition de tous les chiffres qui le constituent. L’opération peut être renouvelée jusqu’à ce qu’on obtienne un résultat à un unique chiffre. Par exemple, la racine numérique de 765 est 9 car
7 + 6 + 5 = 18 et 1 + 8 = 9. Stewart James a montré que, si on considère la racine numérique des termes d’une suite de Fibonacci, alors :
• une telle suite a une période cyclique de 24 termes ;
• chaque période totalise une somme de presque toujours 117.
Reprenons en effet la suite de Fibonacci engendrée par 5 et 7. On peut écrire la suite (un) des racines numériques correspondantes :
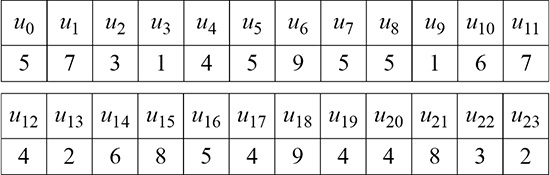
On vérifie facilement que u24 = 5 et u25 = 7 et donc que la suite est de cycle 24.
Remarquons également que
Néanmoins, la formulation du résultat est étrange : la somme est « presque toujours » 117.
Face à l’absence d’une parfaite rigueur mathématique intervient l’ingéniosité du magicien…
Il est possible d’affiner ce résultat de la manière suivante : si la première paire de chiffres est n’importe quelle combinaison de 3, 6 et 9, les 24 termes consécutifs ont un total égal à 135, sauf si la première paire est 9, 9.
Ces constatations suggèrent immédiatement un tour de prédiction, mais avec ce défaut qu’en cas de répétition, le total est presque toujours 117 et parfois 135.
Stewart James a trouvé une parade. Si l’on somme les 25 premiers termes, la somme S sera :
S = u0 + 117 si u0 est différent de 3, 6 ou 9 ;
S = u0 + 135 sinon.
Maintenant que nous avons établi le contexte, passons au tour inventé par Martin Gardner.
Le magicien fournit une grille carrée vide 5 × 5. Il demande à un spectateur de penser à un chiffre de 1 à 9 et de l’inscrire dans la première case et de recommencer avec la case suivante. Pendant ce temps, il tourne le dos au spectateur pour ne pas voir ce qu’il écrit. Il lui demande ensuite de compléter la grille par les racines numériques de la suite de Fibonacci générée par les deux premiers chiffres.
Par exemple, si les deux premiers nombres sont 3 et 4, on obtient la grille ci-dessous.
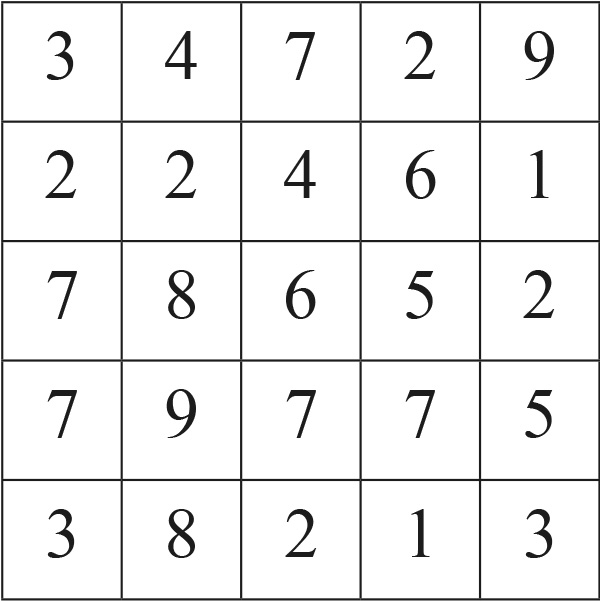
Une fois le carton complété, le magicien propose un petit jeu au spectateur : être le premier à donner la somme de tous les chiffres de la grille. Il lui autorise l’utilisation de la calculatrice. Il va sans dire qu’il annonce le résultat en un claquement de doigts, pour cela, il lui suffit de regarder le premier nombre de la grille (ici 3) et d’annoncer 120, soit 117 + 3 !
[/encadre]
Yves Meret est professeur de mathématiques et magicien professionnel.












