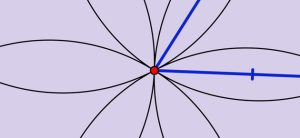
Qu’est-ce qu’un polygone ?

Tout le monde a l’intuition qu’un polygone est composé de points et de segments rectilignes. Mais lorsqu’on se préoccupe d’élaborer une définition mathématique rigoureuse, on se heurte à une multitude de cas « pathologiques ». Il a fallu sortir du cadre géométrique pour aboutir à la notion de polygone « abstrait ».
Premières définitions
Un polygone, ou n-gone, est une séquence cyclique ordonnée de nsommetsS1, S2, …, Sn choisis arbitrairement. Les côtés du polygone sont les segments Ai définis par des paires de sommets adjacents Si, Si+1.
Cette définition générale a été donnée pour la première fois en 1769 par Albrecht Ludwig Friedrich Meister (1724-1788), qui nous est principalement connu par l’historien des mathématiques Siegmund Günther (1848-1923). Ce dernier affirme néanmoins, sans fondement, qu’Albert Girard (1595-1632) avait déjà cette perception du « polygone » dans un ouvrage de 1626, mais il semble qu’il n’ait pas toujours bien compris le texte de Meister.
Cette définition, naturelle et simplissime en apparence, autorise cependant des configurations inattendues et contre-intuitives en n’excluant pas certains cas pathologiques. Ainsi, rien n’interdit à des sommets d’être confondus, ou à des côtés de se chevaucher. Meister en est conscient puisque qu’il présente, dans son ouvrage, un ennéagone (polygone à 9 côtés) de sommets abcABCαβγ, qui semblent être constitué de trois triangles superposés.
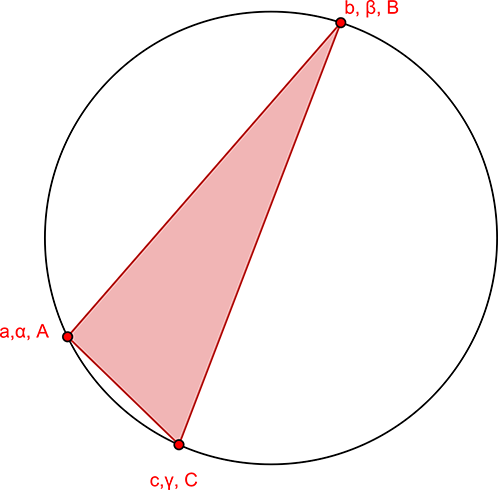
L’ennéagone de Meister.
Louis Poinsot (1777-1859) donne, lui aussi, une définition des polygones. Celle-ci est équivalente à celle de Meister : « Soient m points a, b, c, d, e, etc. rangés comme on voudra dans un plan j’appelle polygone la figure formée par la suite continue des m droits ab, bc, cd, etc., qui joignent tous ces points deux à deux, de manière que la figure soit fermée. » Ainsi, Poinsot, comme la plupart des auteurs suivants, ne précise toujours pas que les sommets sont des points distincts. Quelques auteurs, comme Max Brückner (1860-1934) ou Harold Scott MacDonald Coxeter (1907-2003), l’excluent implicitement, en évitant ce cas de figure dans tous leurs exemples, mais d’autres, comme Henry Martyn Cundy (1913-2005) et Arthur Percy Rollett (1902-1968), prennent le soin de l’écrire explicitement.
Nous allons voir les avantages que l’on peut tirer de l’élémentaire définition de Meister, malheureusement ignorée jusqu’à ce que le mathématicien Branko Grünbaum (1929-2018) la remette à l’honneur. En tout premier lieu, on peut caractériser deux types de polygones : le polygone abstrait et le polygone géométrique.
Un polygone abstrait
Un polygone abstrait est un circuit simple fixe constitué d’un ensemble S cyclique ordonné d’éléments, les sommets, et un ensemble A de paires non ordonnées d’éléments adjacents de S, les arêtes.
On écrit, par exemple, S = {s1, s2, s3, s4} et A = {(s1, s2), (s2, s3), (s3, s4), (s4, s1)}.
Un circuit est un graphe dont la suite d’arcs commence et se termine sur un même sommet. Le terme « simple » signifie que le même arc n’est emprunté qu’une seule fois, et les arêtes non ordonnées n’ont pas de sens privilégié de parcours. Un polygone abstrait étant un graphe, sa définition emprunte naturellement le vocabulaire de la théorie des graphes.
On peut aussi définir un polygone abstrait comme un circuit eulérien simple, c’est-à-dire passant par toutes les arêtes, une seule fois, ce qui nécessite un nombre pair d’arêtes en chaque sommet, et par conséquent au moins trois sommets.
Pour dessiner un polygone abstrait, il suffit de dessiner le graphe en numérotant les sommets dans leur ordre d’apparition dans l’ensemble cyclique des éléments ordonnés.
Un polygone abstrait avec autant de sommets que d’arêtes est dit unicursal.
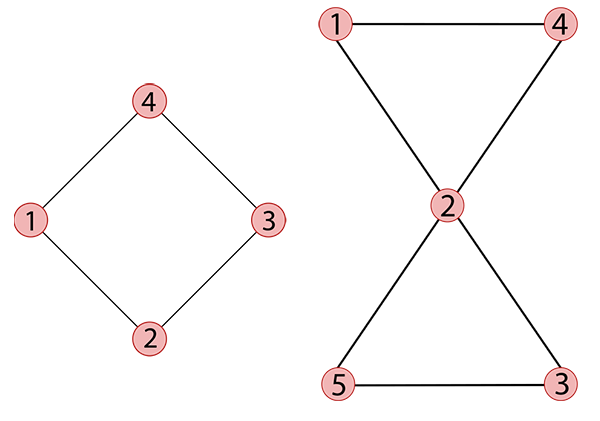
Polygones abstraits, unicursal à gauche et non unicursal à droite.
Cette façon « abstraite » de représenter les polygones comme des graphes particuliers permet de bénéficier de tout le corpus théorique de la théorie des graphes.
Le polygone géométrique
Un polygone géométrique, ou tout simplement polygone, est l’image d’un polygone abstrait par une application qui matérialise chaque sommet du polygone abstrait par un point de l’espace.
Cette définition généralise la notion « naïve » de polygone et intègre de nombreux cas particuliers. Dans cette définition, rien n’interdit de faire correspondre un même point à plusieurs sommets abstraits. L’application n’est pas supposée injective. De plus cette définition ne donne aucune contrainte, ni sur les sommets ni sur les côtés.
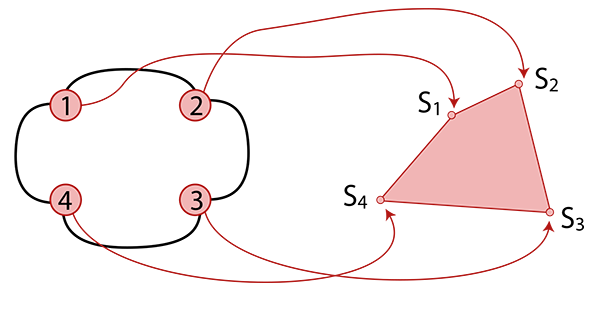
Un polygone abstrait matérialisé en polygone géométrique.
Il existe un cas particulier dégénéré où l’image de tous les sommets abstraits est un même sommet géométrique.
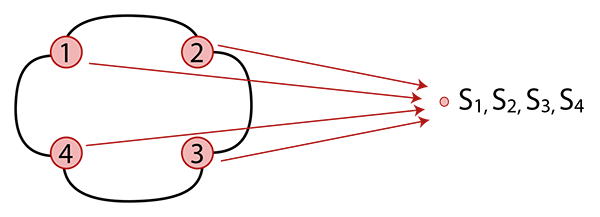
Polygone dégénéré.
L’ensemble d’arrivée de notre application ne se restreint pas forcément à un plan, et peut être une partie quelconque de l’espace. Dans ce cas, nous parlerons de polygones gauches. Dans la suite, sauf mention explicite, tous les sommets d’un polygone seront dans un même plan.
Coïncidences
La définition précédente autorise toutes sortes de coïncidences de sommets, adjacents ou non, et de superpositions d’arêtes. Une arête peut contenir plus de deux sommets et un polygone peut être entièrement contenu dans une droite.
Le mathématicien allemand August Ferdinand Möbius (1790-1868) exclut ce cas dans ses travaux sur les polygones.
Les différents types de polygones possibles peuvent être caractérisés par les définitions suivantes :
• Un polygone est dit ordinaire s’il n’existe pas d’ensemble de trois arêtes ayant un point commun. Dans un polygone ordinaire, deux côtés ont soit aucun point en commun, soit un seul lorsqu’ils se croisent ou si ces deux côtés sont consécutifs. Dans ce dernier cas, le point commun est un sommet. Lorsque deux côtés se croisent, le polygone est croisé. Certains polygones croisés sont ordinaires.
• Un polygone est acoptique, du grec κοπτω (kóptō, « couper »), si les côtés ne se coupent pas. Les polygones croisés sont non acoptiques.
• Un polygone ordinaire et acoptique est simple. Dans un polygone simple, seuls les côtés adjacents possèdent un point commun, un sommet. Les polygones simples sont des courbes de Jordan, c’est-à-dire qu’ils définissent un intérieur, borné (par définition), et un extérieur.
• Un polygone est aploïque, du grec απλοοσ (aplóos, « sans complication ») si les sommets sont distincts et les arêtes ne se superposent pas. Les polygones aploïques définissent une surface intérieure non nulle.
• Un polygone non aploïque n’est pas toujours ordinaire bien que ces deux notions soient proches. Parmi les polygones croisés il existe des cas très proches des polygones simples, la notion d’aploïque permet de traiter ces cas.

Polygone non ordinaire aploïque.
Cette terminologie grecque a été introduite par Branko Grünbaum, un mathématicien contemporain qui s’est beaucoup intéressé aux graphes, polygones et pavages.
Dans les polygones simples, il peut tout de même exister des cas pathologiques. C’est le cas quand deux côtés sont dans le prolongement l’un de l’autre, ce qui nécessite la définition de la notion de sommet propre :
Le sommet d’un polygone est propre s’il n’appartient pas à deux cotés colinéaires. Un polygone est propre si tous ses sommets sont propres.
Un polygone non aploïque peut être entièrement contenu sur une droite. Dans le cas contraire, on parle de polygone de pleine dimension.
Voici, à titre d’illustration, les différents quadrilatères que l’on peut obtenir à partir du polygone abstrait ci-dessous :
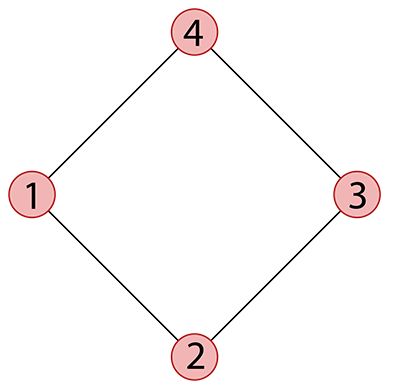
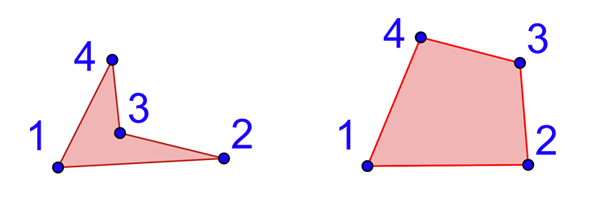
Propres, acoptiques, ordinaires, aploïques.
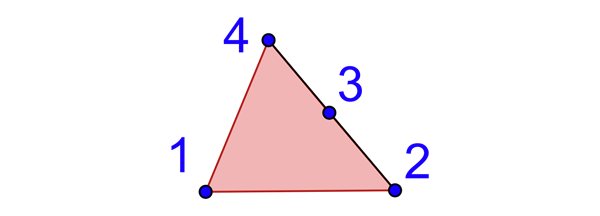
Non propre, acoptique, ordinaire, aploïque.
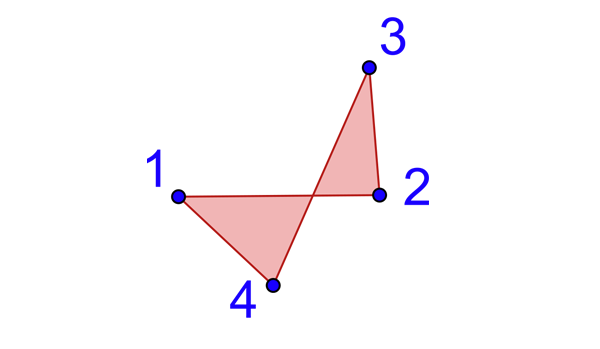
Propre, non acoptique, ordinaire, aploïque.
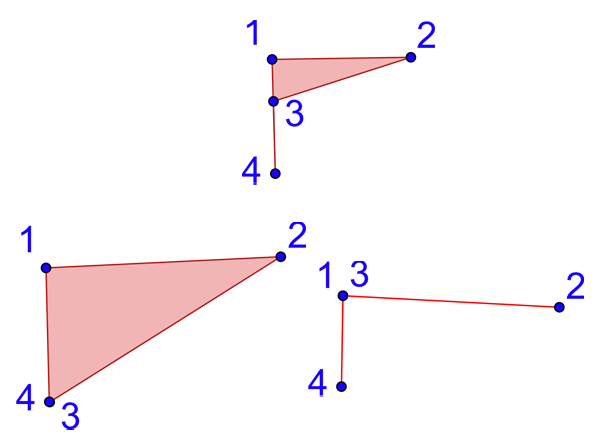
Non ordinaires et non aploïques.
Si tous ces polygones sont en pleine dimension, les suivants ne le sont pas :
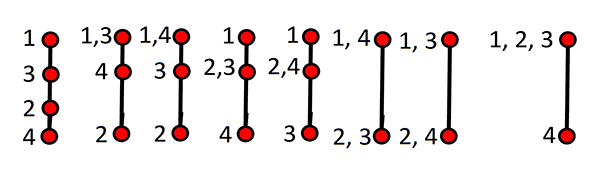
Dans la plupart des cas, nous traiterons, dans ce numéro, de polygones ordinaires, aploïques, voir acoptiques ou même simples. Mais il est intéressant de savoir qu’il en existe d’autres. On observera, par exemple, lors d’une transformation continue, l’apparition, à certaines étapes, de polygones qui ne semblent pas correspondre à la conception habituelle (voir en page 14). Mais l’essentiel est de savoir à quel type de polygone nous avons affaire.